Centered Dodecagonal Number
Last Updated :
20 May, 2022
Given a number n, find the nth Centered Dodecagonal Number.
The Centered Dodecagonal Number represents a dot in the center and other dots surrounding it in successive dodecagonal(12 sided polygon) layers.
Examples :
Input : 3
Output : 37
Input : 7
Output :253

The first few centered dodecagonal numbers are:
1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661…………………..
The formula for the nth Centered dodecagonal number:
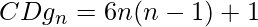
C++
#include <bits/stdc++.h>
using namespace std;
int centeredDodecagonal(long int n)
{
return 6 * n * (n - 1) + 1;
}
int main()
{
long int n = 2;
cout << centeredDodecagonal(n);
cout << endl;
n = 9;
cout << centeredDodecagonal(n);
return 0;
}
|
C
#include <stdio.h>
int centeredDodecagonal(long int n)
{
return 6 * n * (n - 1) + 1;
}
int main()
{
long int n = 2;
printf("%d\n",centeredDodecagonal(n));
n = 9;
printf("%d\n",centeredDodecagonal(n));
return 0;
}
|
Java
import java.io.*;
class GFG{
static long centeredDodecagonal(long n)
{
return 6 * n * (n - 1) + 1;
}
public static void main(String[] args)
{
long n = 2;
System.out.println(centeredDodecagonal(n));
n = 9;
System.out.println(centeredDodecagonal(n));
}
}
|
Python3
def centeredDodecagonal(n) :
return 6 * n * (n - 1) + 1;
n = 2
print(centeredDodecagonal(n));
n = 9
print(centeredDodecagonal(n));
|
C#
using System;
class GFG{
static long centeredDodecagonal(long n)
{
return 6 * n * (n - 1) + 1;
}
public static void Main(String[] args)
{
long n = 2;
Console.WriteLine(centeredDodecagonal(n));
n = 9;
Console.WriteLine(centeredDodecagonal(n));
}
}
|
Javascript
<script>
function centeredDodecagonal(n)
{
return 6 * n * (n - 1) + 1;
}
let n = 2;
document.write(centeredDodecagonal(n));
document.write("<br>");
n = 9;
document.write(centeredDodecagonal(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
References
http://oeis.org/A003154
Share your thoughts in the comments
Please Login to comment...