Basis Path Testing in Software Testing
Last Updated :
15 Dec, 2022
Prerequisite – Path Testing Basis Path Testing is a white-box testing technique based on the control structure of a program or a module. Using this structure, a control flow graph is prepared and the various possible paths present in the graph are executed as a part of testing. Therefore, by definition, Basis path testing is a technique of selecting the paths in the control flow graph, that provide a basis set of execution paths through the program or module. Since this testing is based on the control structure of the program, it requires complete knowledge of the program’s structure. To design test cases using this technique, four steps are followed :
- Construct the Control Flow Graph
- Compute the Cyclomatic Complexity of the Graph
- Identify the Independent Paths
- Design Test cases from Independent Paths
Let’s understand each step one by one. 1. Control Flow Graph – A control flow graph (or simply, flow graph) is a directed graph which represents the control structure of a program or module. A control flow graph (V, E) has V number of nodes/vertices and E number of edges in it. A control graph can also have :
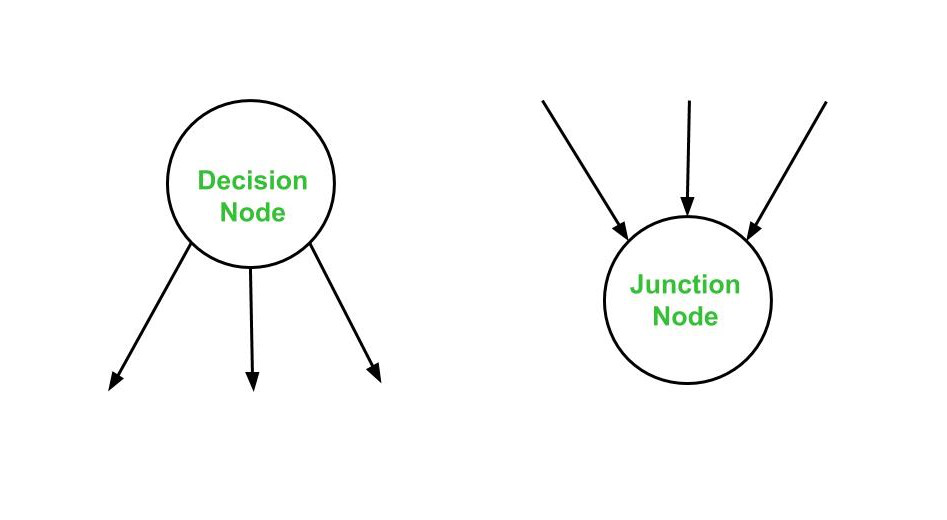
- Junction Node – a node with more than one arrow entering it.
- Decision Node – a node with more than one arrow leaving it.
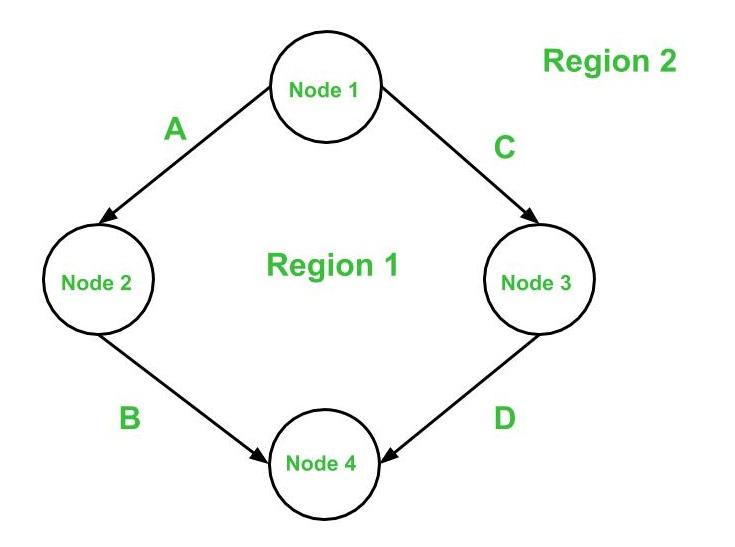
- Region – area bounded by edges and nodes (area outside the graph is also counted as a region.).
 Below are the notations used while constructing a flow graph :
Below are the notations used while constructing a flow graph :
- Sequential Statements –

- If – Then – Else –

- Do – While –

- While – Do –

- Switch – Case –

Cyclomatic Complexity – The cyclomatic complexity V(G) is said to be a measure of the logical complexity of a program. It can be calculated using three different formulae :
- Formula based on edges and nodes :
V(G) = e - n + 2*P
- Where, e is number of edges, n is number of vertices, P is number of connected components. For example, consider first graph given above,
where, e = 4, n = 4 and p = 1
So,
Cyclomatic complexity V(G)
= 4 - 4 + 2 * 1
= 2
- Formula based on Decision Nodes :
V(G) = d + P
- where, d is number of decision nodes, P is number of connected nodes. For example, consider first graph given above,
where, d = 1 and p = 1
So,
Cyclomatic Complexity V(G)
= 1 + 1
= 2
- Formula based on Regions :
V(G) = number of regions in the graph
- For example, consider first graph given above,
Cyclomatic complexity V(G)
= 1 (for Region 1) + 1 (for Region 2)
= 2
Hence, using all the three above formulae, the cyclomatic complexity obtained remains same. All these three formulae can be used to compute and verify the cyclomatic complexity of the flow graph. Note –
- For one function [e.g. Main( ) or Factorial( ) ], only one flow graph is constructed. If in a program, there are multiple functions, then a separate flow graph is constructed for each one of them. Also, in the cyclomatic complexity formula, the value of ‘p’ is set depending of the number of graphs present in total.
- If a decision node has exactly two arrows leaving it, then it is counted as one decision node. However, if there are more than 2 arrows leaving a decision node, it is computed using this formula :
d = k - 1
- Here, k is number of arrows leaving the decision node.
Independent Paths : An independent path in the control flow graph is the one which introduces at least one new edge that has not been traversed before the path is defined. The cyclomatic complexity gives the number of independent paths present in a flow graph. This is because the cyclomatic complexity is used as an upper-bound for the number of tests that should be executed in order to make sure that all the statements in the program have been executed at least once. Consider first graph given above here the independent paths would be 2 because number of independent paths is equal to the cyclomatic complexity. So, the independent paths in above first given graph :
A -> B
C -> D
Note – Independent paths are not unique. In other words, if for a graph the cyclomatic complexity comes out be N, then there is a possibility of obtaining two different sets of paths which are independent in nature. Design Test Cases : Finally, after obtaining the independent paths, test cases can be designed where each test case represents one or more independent paths. Advantages : Basis Path Testing can be applicable in the following cases:
- More Coverage – Basis path testing provides the best code coverage as it aims to achieve maximum logic coverage instead of maximum path coverage. This results in an overall thorough testing of the code.
- Maintenance Testing – When a software is modified, it is still necessary to test the changes made in the software which as a result, requires path testing.
- Unit Testing – When a developer writes the code, he or she tests the structure of the program or module themselves first. This is why basis path testing requires enough knowledge about the structure of the code.
- Integration Testing – When one module calls other modules, there are high chances of Interface errors. In order to avoid the case of such errors, path testing is performed to test all the paths on the interfaces of the modules.
- Testing Effort – Since the basis path testing technique takes into account the complexity of the software (i.e., program or module) while computing the cyclomatic complexity, therefore it is intuitive to note that testing effort in case of basis path testing is directly proportional to the complexity of the software or program.
Share your thoughts in the comments
Please Login to comment...