Banking of Road Formula

Last Updated : 23 Mar, 2022

For a vehicle going at high speed along a curved road, banking of road is the ideal solution. The outside edge of a road is pushed up during a curve, making it higher than the inner edge, and the road surface resembles a gently inclined plane for the vehicle’s safety. This process is referred to as road banking or the banking of road.

In other words, Banking of Road refers to the technique of lifting the outside border (edge) of a road above its inner border (edge) at a specific angle (the angle here is known as banking angle).

Necessity of banking of road

When the vehicle is moving along a curved road, the centripetal force must be provided, otherwise, there is a danger of throwing the vehicle away tangentially.
The frictional force between the wheels and the road can provide centripetal force, but the safe speed for such roads is very low and is not reliable.
In the Banking of roads, the horizontal component of normal reaction provides the necessary centripetal force, and vehicles are protected from accidents.

Formulae related to Banking of Roads

The velocity of a vehicle on a curved banked road: v = $\sqrt{(\frac{Rg(μs + tanθ)}{(1−μs tanθ)}}$
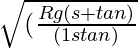
For a given pair of roads, and Tyre μ_s= tanλ, then the velocity of a vehicle on a curved banked road is: v = $\sqrt{Rg tan(θ + λ)}$
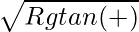
The safe velocity on an unbanked road is: v_max = $\sqrt{μ Rg}$
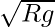
The expression for the angle of banking of road is: θ = tan^-1[v₀² / Rg]
Expression for the safe velocity on the banked road is: v_max = $\sqrt{rg tanθ}$

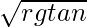
Derivation for all the formulae is given below,

Derivations

Consider the above figure, where

mg = weight of vehicle

N = Normal reaction

f = Frictional Force

f cosθ = Horizontal component of Frictional Force

f sinθ = Vertical component of Frictional Force

N cosθ = vertical component of Normal Reaction

N sinθ = Horizontal component of Normal Reaction

Consider a vehicle of mass m moving with velocity v along a curved banked road banked at an angle θ. Let f be the frictional force between the tires of the vehicle and the surface of the road.

The forces acting on the vehicle are,

Weight mg acting vertically downward
Normal reaction N in upward reaction through the center of gravity and perpendicular to banked road/surface.

The frictional force between the tires of the vehicle and road surface can be resolved into,

f cosθ – along the horizontal direction
f sinθ – along a vertically downward direction

The normal reaction can be resolved into two components,

N cosθ – Vertical component of normal reaction
N sinθ – Horizontal component of normal reaction

The component N cosθ of Normal Reaction is balanced by weight mg of vehicle and component f sinθ of frictional force,

N cosθ = mg + f sinθ

∴ mg = N cosθ – f sinθ ⇢ (1)

Horizontal component N sinθ along with component f cosθ of frictional force provides the necessary centripetal force.

N sinθ + f cosθ = mv²/ R

Or, mv²/ R = N sinθ + f cosθ ⇢ (2)

Dividing Eq (2) by Eq (1),

v²/ Rg = N sinθ + f cosθ / N cosθ – f sinθ ⇢ (3)

The magnitude of the frictional force depends on the speed of the vehicle for a given road surface and the tires of the vehicle. Let v_max denote the maximum speed of the vehicle, the frictional force f_mproduced at this speed should be

f_m= μ_sN ⇢ (4)

v²_max / Rg = N sinθ + f cosθ / N cosθ – f sinθ ⇢ (5)

From Eq (4) and Eq (5), we get v_max

∴ v_max = $\sqrt{\frac{Rg[( μs + tanθ)}{(1 - μs tanθ) ]}}$ ⇢ (6)

For a curved Horizontal road, θ = 0°, hence Eq (6) becomes,

v_max = √{μ Rg} ⇢ (7)

Now, if we compare Eq (6) and Eq (7) it is revealed that the maximum safe speed of vehicles on a banked road is greater than that of a curved horizontal road/level road.

If μ_s = 0, then Eq (6) becomes

v_max = v₀ = 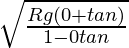$\sqrt{\frac{Rg (0 + tanθ)}{1 - 0 tanθ }}$

v₀ = 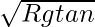$\sqrt{Rg tanθ}$ ⇢ (8)

At this speed, the Frictional force is not needed to provide the necessary centripetal force. there will be a little water and tear of the tire if the vehicle is driven at this speed on the banked road. v₀ is called optimum speed.

From Eq (8), i.e.

v₀ = 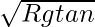$\sqrt{Rg tanθ}$

tanθ = v₀² / Rg

θ = tan^-1[v₀² / Rg] ⇢ (9)

Note: This formula [Eq (9)] for angle of banking does not involves mass of vehicle m. Thus the angle of banking is independent of mass of vehicle.

Sample Problems

Question 1: Find the maximum speed of a car with which it can be safely driven along a curve of radius 100m and the coefficient of friction between tires and road is 0.2. (take g = 9.8 m/s²)

Solution:

Given data:

Radius (r) = 100m
Coefficient of friction (μ) = 0.2
Gravity (g) = 9.8 m/s²
Formula: v= √(μrg)

v = √(μrg)

= √(0.2 × 100 × 9.8)

= √196

v = 14 m/s

Thus maximum speed of car is 14 m/s.

Question 2: Calculate the maximum speed with which a car can be driven safely along a curved road of a radius of 30m and banked at an angle of 30° with the horizontal. (take g = 9.8m/s²)

Given data:

Radius (r) = 30m
Angle of banking of road (θ) = 30°
Gravity (g) = 9.8 m/s²
Formula: v= √rg tanθ

v= 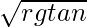$\sqrt{rg tanθ}$

= $\sqrt{30 × 9.8 × tan 30° }$

= $\sqrt{30 × 9.8 × 0.5774}$

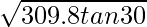
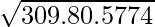
v = 13.03 m/s

Thus the maximum speed of car is 13.03 m/s

Question 3: Find the angle which the bicycle and its rider make with the vertical when going at 18 km/hr around a curved road of radius 10m on level ground. (take g = 9.8 m/s²)

Given data:

Radius (r) = 10 m
Max speed of rider (v) = 18 km/hr
Gravity (g) = 9.8 m/s²
Formula: tanθ = v² / rg

v = 18 km/hr

= 18 × 1000 / 3600

= 5 m/s

Tangent angle of banking is tanθ = v² / rg

= 5 × 5 / 10 × 9.8

= 5 / 2 × 9.8

tanθ = 0.251

θ = tan^-1 (0.2551)

θ = 14° 19^‘

Thus the angle which the bicycle and rider make is 14° 19^‘

Question 4: A motor van weighing 4400kg rounds a level curve of radius 200m on the unbanked road at 60km/hr. What should be the minimum value of the coefficient of friction to prevent skidding? At what angle the road should be banked for this velocity.

Given data:

Weight of van (m) = 4400kg
Radius (r) = 200m
Speed of van (v) = 60km/hr
Gravity (g) = 9.8m/s²

v = 60km/hr

= 60 × 1000 / 3600

= 50 / 3 m/s

To prevent skidding, mv² / r = μmg

μ = v² / rg

= (50 / 3)² / 200 × 9.8

= 25 / 18 × 9.8

μ = 0.1417

Banking angle tanθ is = v² / rg

= (50 / 3)² / 200 × 9.8

tanθ = 0.1417

θ = tan^-1(0.1417)

θ = 8° 4^‘

Thus the coefficient of friction is 0.1417 and the angle of banking is 8° 4^‘.

Question 5: A circular racecourse track has a radius of 500 m and is banked to 100. If the coefficient of friction between tires of the vehicle and the road surface is 0.25. Compute the maximum speed to avoid slipping of the car and the optimum speed to avoid wear and tear of tires. (take g = 9.8 m/s²)

Given data:

Radius (r) = 500m
Angle (θ) = 10°
Coefficient of Friction (μ) = 0.25

since, θ = 10°

tan10° = 0.1763

On the banked racecourse track, the maximum speed to avoid slipping,

v_max = 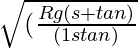$\sqrt{(\frac{Rg(μs + tanθ)}{(1−μs tanθ)}}$

= $\sqrt{\frac{500 × 9.8(0.25 + 0.1763)}{(1 - (0.25 × 0.1763))}}$

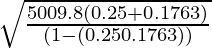
= √{500 × 9.8 × 0.4263 / 0.9559}

= √2185

v_max = 46.75 m/s

The optimum speed of the vehicle on track is given by v_opt = 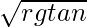$\sqrt{rg tanθ}$

= $\sqrt{500 × 9.8 × 0.1763}$

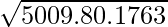
= √863.9

v_opt = 29.39 m/s

Question 6: Find the banking angle of the railway track with a radius of curvature of 1500m. If the train’s maximum speed is 15m/s. If the distance between the two tracks is 1.8m, calculate the elevation of the outer track over the inner track.

Given data:

Radius (r) = 1500m
Velocity (v) = 15m/s
Distance between two tracks (l) = 1.8m

Tangent angle of Banking ,

tanθ = v² / rg

= 15 × 15 / 1500 × 9.8

= 0.015306

θ = tan^-1(0.0153)

θ = 0° 52‘

Consider the above figure,

sinθ = h / l

h = l × sinθ

= 1.8 × sin(0° 52‘)

= 1.8 × 0.0157

h = 0.02826

The banking angle is 0° 52‘ and the elevation of the outer track over inner track is 0.02826.

Question 7: A meter gauge train is moving at 60 km/Hr along a curved road of a radius of curvature of 500m at a certain place. Find the elevation of the outer rail above the inner rail, so that there is no side pressure on the rail (take g = 9.8m/s²)

Given data:

Velocity (v) = 60Km/Hr = 50 / 3 m/s
Radius (r) = 500m
l = 1m

In case of Banked railway track,

tanθ = v² / rg

= ( 50 / 3 )² / 500 × 9.8

= 0.05670

θ = tan^-1(0.05670)

θ = 3° 15‘

Elevation of the outer rail above the inner rail,

h = l sinθ

= (1) sin(3° 15‘)

h = 0.0567m