Array range queries for searching an element
Last Updated :
27 Apr, 2023
Given an array of N elements and Q queries of the form L R X. For each query, you have to output if the element X exists in the array between the indices L and R(included).
Prerequisite : Mo’s Algorithms
Examples :
Input : N = 5
arr = [1, 1, 5, 4, 5]
Q = 3
1 3 2
2 5 1
3 5 5
Output : No
Yes
Yes
Explanation :
For the first query, 2 does not exist between the indices 1 and 3.
For the second query, 1 exists between the indices 2 and 5.
For the third query, 5 exists between the indices 3 and 5.
Naive Approach :
The naive method would be to traverse the elements from L to R for each query, linearly searching for X. In the worst case, there can be N elements from L to R, hence the worst case time complexity for each query would be O(N). Therefore, for all the Q queries, the time complexity would turn out to be O(Q*N).
Using Union-Find Method :
This method checks only one element among all the consecutive equal values. If X is not equal to these values, then the algorithm skips all the other the other equal elements and continues traversal with the next different element. This algorithm is evidently useful only when there are consecutive equal elements in large amounts.
Algorithm :
- Merge all the consecutive equal elements in one group.
- While processing a query, start from R. Let index = R.
- Compare a[index] with X. If they are equal, then print “Yes” and break out of traversing the rest of the range. Else, skip all the consecutive elements belonging to the group of a[index]. Index becomes equal to one less than the index of the root of this group.
- Continue the above step either till X is found or till index becomes less than L.
- If index becomes less than L, print “No”.
Below is the implementation of the above idea.
C++
#include <bits/stdc++.h>
using namespace std;
struct Query
{
int L, R, X;
};
const int maxn = 100;
int root[maxn];
int find(int x)
{
return x == root[x] ? x : root[x] =
find(root[x]);
}
int uni(int x, int y)
{
int p = find(x), q = find(y);
if (p != q) {
root[p] = root[q];
}
}
void initialize(int a[], int n, Query q[], int m)
{
for (int i = 0; i < n; i++)
root[i] = i;
for (int i = 1; i < n; i++)
if (a[i] == a[i - 1])
uni(i, i - 1);
}
int main()
{
int a[] = { 1, 1, 5, 4, 5 };
int n = sizeof(a) / sizeof(a[0]);
Query q[] = { { 0, 2, 2 }, { 1, 4, 1 },
{ 2, 4, 5 } };
int m = sizeof(q) / sizeof(q[0]);
initialize(a, n, q, m);
for (int i = 0; i < m; i++)
{
int flag = 0;
int l = q[i].L, r = q[i].R, x = q[i].X;
int p = r;
while (p >= l)
{
if (a[p] == x)
{
flag = 1;
break;
}
p = find(p) - 1;
}
if (flag != 0)
cout << x << " exists between [" << l
<< ", " << r << "] " << endl;
else
cout << x << " does not exist between ["
<< l << ", " << r << "] " << endl;
}
}
|
Java
import java.util.*;
class GFG
{
static class Query
{
int L, R, X;
public Query(int L, int R, int X)
{
this.L = L;
this.R = R;
this.X = X;
}
};
static int maxn = 100;
static int []root = new int[maxn];
static int find(int x)
{
if(x == root[x])
return x;
else
return root[x] = find(root[x]);
}
static void uni(int x, int y)
{
int p = find(x), q = find(y);
if (p != q)
{
root[p] = root[q];
}
}
static void initialize(int a[], int n,
Query q[], int m)
{
for (int i = 0; i < n; i++)
root[i] = i;
for (int i = 1; i < n; i++)
if (a[i] == a[i - 1])
uni(i, i - 1);
}
public static void main(String args[])
{
int a[] = { 1, 1, 5, 4, 5 };
int n = a.length;
Query q[] = { new Query(0, 2, 2 ),
new Query( 1, 4, 1 ),
new Query( 2, 4, 5 ) };
int m = q.length;
initialize(a, n, q, m);
for (int i = 0; i < m; i++)
{
int flag = 0;
int l = q[i].L, r = q[i].R, x = q[i].X;
int p = r;
while (p >= l)
{
if (a[p] == x)
{
flag = 1;
break;
}
p = find(p) - 1;
}
if (flag != 0)
System.out.println(x + " exists between [" +
l + ", " + r + "] ");
else
System.out.println(x + " does not exist between [" +
l + ", " + r + "] ");
}
}
}
|
Python3
class Query:
def __init__(self, L, R, X):
self.L = L
self.R = R
self.X = X
maxn = 100
root = [0] * maxn
def find(x):
if x == root[x]:
return x
else:
root[x] = find(root[x])
return root[x]
def uni(x, y):
p = find(x)
q = find(y)
if p != q:
root[p] = root[q]
def initialize(a, n, q, m):
for i in range(n):
root[i] = i
for i in range(1, n):
if a[i] == a[i - 1]:
uni(i, i - 1)
if __name__ == "__main__":
a = [1, 1, 5, 4, 5]
n = len(a)
q = [Query(0, 2, 2),
Query(1, 4, 1),
Query(2, 4, 5)]
m = len(q)
initialize(a, n, q, m)
for i in range(m):
flag = False
l = q[i].L
r = q[i].R
x = q[i].X
p = r
while p >= l:
if a[p] == x:
flag = True
break
p = find(p) - 1
if flag:
print("%d exists between [%d, %d]" % (x, l, r))
else:
print("%d does not exists between [%d, %d]" % (x, l, r))
|
C#
using System;
class GFG
{
public class Query
{
public int L, R, X;
public Query(int L, int R, int X)
{
this.L = L;
this.R = R;
this.X = X;
}
};
static int maxn = 100;
static int []root = new int[maxn];
static int find(int x)
{
if(x == root[x])
return x;
else
return root[x] = find(root[x]);
}
static void uni(int x, int y)
{
int p = find(x), q = find(y);
if (p != q)
{
root[p] = root[q];
}
}
static void initialize(int []a, int n,
Query []q, int m)
{
for (int i = 0; i < n; i++)
root[i] = i;
for (int i = 1; i < n; i++)
if (a[i] == a[i - 1])
uni(i, i - 1);
}
public static void Main(String []args)
{
int []a = { 1, 1, 5, 4, 5 };
int n = a.Length;
Query []q = {new Query(0, 2, 2),
new Query(1, 4, 1),
new Query(2, 4, 5)};
int m = q.Length;
initialize(a, n, q, m);
for (int i = 0; i < m; i++)
{
int flag = 0;
int l = q[i].L, r = q[i].R, x = q[i].X;
int p = r;
while (p >= l)
{
if (a[p] == x)
{
flag = 1;
break;
}
p = find(p) - 1;
}
if (flag != 0)
Console.WriteLine(x + " exists between [" +
l + ", " + r + "] ");
else
Console.WriteLine(x + " does not exist between [" +
l + ", " + r + "] ");
}
}
}
|
Javascript
<script>
class Query
{
constructor(L, R, X)
{
this.L = L;
this.R = R;
this.X = X;
}
};
let maxn = 100;
let root = new Array(maxn);
function find(x)
{
if(x == root[x])
return x;
else
return root[x] = find(root[x]);
}
function uni(x, y)
{
let p = find(x), q = find(y);
if (p != q)
{
root[p] = root[q];
}
}
function initialize(a, n, q, m)
{
for (let i = 0; i < n; i++)
root[i] = i;
for (let i = 1; i < n; i++)
if (a[i] == a[i - 1])
uni(i, i - 1);
}
let a = [ 1, 1, 5, 4, 5 ];
let n = a.length;
let q = [ new Query(0, 2, 2 ),
new Query( 1, 4, 1 ),
new Query( 2, 4, 5 ) ];
let m = q.length;
initialize(a, n, q, m);
for (let i = 0; i < m; i++)
{
let flag = 0;
let l = q[i].L, r = q[i].R, x = q[i].X;
let p = r;
while (p >= l)
{
if (a[p] == x)
{
flag = 1;
break;
}
p = find(p) - 1;
}
if (flag != 0)
document.write(x + " exists between [" +
l + ", " + r + "] " + "<br>");
else
document.write(x + " does not exist between [" +
l + ", " + r + "] " + "<br>");
}
</script>
|
Output2 does not exist between [0, 2]
1 exists between [1, 4]
5 exists between [2, 4]
Efficient Approach(Using Mo’s Algorithm) :
Mo’s algorithm is one of the finest applications for square root decomposition.
It is based on the basic idea of using the answer to the previous query to compute the answer for the current query. This is made possible because the Mo’s algorithm is constructed in such a way that if F([L, R]) is known, then F([L + 1, R]), F([L – 1, R]), F([L, R + 1]) and F([L, R – 1]) can be computed easily, each in O(F) time.
Answering queries in the order they are asked, then the time complexity is not improved to what is needed to be. To reduce the time complexity considerably, the queries are divided into blocks and then sorted.
The exact algorithm to sort the queries is as follows :
- Denote BLOCK_SIZE = sqrt(N)
- All the queries with the same L/BLOCK_SIZE are put in the same block
- Within a block, the queries are sorted based on their R values
- The sort function thus compares two queries, Q1 and Q2 as follows:
Q1 must come before Q2 if: - L1/BLOCK_SIZE<L2/BLOCK_SIZE
- L1/BLOCK_SIZE=L2/BLOCK_SIZE and R1<R2
After sorting the queries, the next step is to compute the answer to the first query and consequently answer rest of the queries. To determine if a particular element exists or not, check the frequency of the element in that range. A non zero frequency confirms the existence of the element in that range.
To store the frequency of the elements, STL map has been used in the following code.
In the example given, first query after sorting the array of queries is {0, 2, 2}. Hash the frequencies of the elements in [0, 2] and then check the frequency of the element 2 from the map. Since, 2 occurs 0 times, print “No”.
While processing the next query, which is {1, 4, 1} in this case, decrement the frequencies of the elements in the range [0, 1) and increment the frequencies of the elements in range [3, 4]. This step gives the frequencies of elements in [1, 4] and it can easily be seen from the map that 1 exists in this range.
Time complexity :
The pre-processing part, that is sorting the queries takes O(m Log m) time.
The index variable for R changes at most 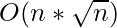 times throughout the run and that for L changes its value at most
times throughout the run and that for L changes its value at most  times. Hence, processing all queries takes
times. Hence, processing all queries takes 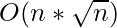 +
+  =
= 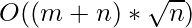 time.
time.
Space complexity:
The space complexity of the given program is O((m+n) * sqrt(n)) where n is the size of the input array a[] and m is the number of queries.
Below is the C++ implementation of the above idea :
C++
#include <bits/stdc++.h>
using namespace std;
int block;
struct Query
{
int L, R, X;
};
bool compare(Query x, Query y)
{
if (x.L / block != y.L / block)
return x.L / block < y.L / block;
return x.R < y.R;
}
void queryResults(int a[], int n, Query q[], int m)
{
block = (int)sqrt(n);
sort(q, q + m, compare);
int currL = 0, currR = 0;
map<int, int> mp;
for (int i = 0; i < m; i++) {
int L = q[i].L, R = q[i].R, X = q[i].X;
while (currL < L)
{
mp[a[currL]]--;
currL++;
}
while (currL > L)
{
mp[a[currL - 1]]++;
currL--;
}
while (currR <= R)
{
mp[a[currR]]++;
currR++;
}
while (currR > R + 1)
{
mp[a[currR - 1]]--;
currR--;
}
if (mp[X] != 0)
cout << X << " exists between [" << L
<< ", " << R << "] " << endl;
else
cout << X << " does not exist between ["
<< L << ", " << R << "] " << endl;
}
}
int main()
{
int a[] = { 1, 1, 5, 4, 5 };
int n = sizeof(a) / sizeof(a[0]);
Query q[] = { { 0, 2, 2 }, { 1, 4, 1 }, { 2, 4, 5 } };
int m = sizeof(q) / sizeof(q[0]);
queryResults(a, n, q, m);
return 0;
}
|
Java
import java.util.*;
class Query{
int L;
int R;
int x;
Query(int L, int R,int x){
this.L = L;
this.R = R;
this.x=x;
}
}
class Main{
static void queryResults(int a[], int n, ArrayList<Query> q, int m){
int block = (int) Math.sqrt(n);
Collections.sort(q, new Comparator<Query>(){
public int compare(Query x, Query y){
if (x.L/block != y.L/block)
return (x.L < y.L ? -1 : 1);
return (x.R < y.R ? -1 : 1);
}
});
int currL = 0, currR = 0;
Map<Integer,Integer> mp=new HashMap<Integer,Integer>();
for (int i=0; i<m; i++)
{
int L = q.get(i).L, R = q.get(i).R, X = q.get(i).x;
while (currL < L)
{
if(mp.containsKey(a[currL])){
mp.put(a[currL],mp.get(a[currL])-1);
}
else{
mp.put(a[currL],1);
}
currL++;
}
while (currL > L)
{
if(mp.containsKey(a[currL-1])){
mp.put(a[currL-1],mp.get(a[currL-1])+1);
}
else{
mp.put(a[currL-1],1);
}
currL--;
}
while (currR <= R)
{
if(mp.containsKey(a[currR])){
mp.put(a[currR],mp.get(a[currR])+1);
}
else{
mp.put(a[currR],1);
}
currR++;
}
while (currR > R+1)
{
if(mp.containsKey(a[currR-1])){
mp.put(a[currR-1],mp.get(a[currR-1])-1);
}
else{
mp.put(a[currR-1],1);
currR--;
}
}
if (mp.containsKey(X))
System.out.println(X + " exists between [" + L +
", " + R + "] ");
else
System.out.println(X + " does not exist between [" + L +
", " + R + "] ");
}
}
public static void main(String argv[]){
ArrayList<Query> q = new ArrayList<Query>();
q.add(new Query(0,2,2));
q.add(new Query(1,4,1));
q.add(new Query(2,4,5));
int a[] = {1, 1, 5, 4, 5 };
queryResults(a, a.length, q, q.size());
}
}
|
Python3
from math import sqrt
def query_results(a, n, q, m):
block = int(sqrt(n))
q = sorted(q, key=lambda x: (x[0] // block, x[1]))
curr_l = 0
curr_r = 0
mp = {}
for i in range(m):
l = q[i][0]
r = q[i][1]
x = q[i][2]
while curr_l < l:
mp[a[curr_l]] -= 1
curr_l += 1
while curr_l > l:
mp[a[curr_l - 1]] = mp.get(a[curr_l - 1], 0) + 1
curr_l -= 1
while curr_r <= r:
mp[a[curr_r]] = mp.get(a[curr_r], 0) + 1
curr_r += 1
while curr_r > r + 1:
mp[a[curr_r - 1]] -= 1
curr_r -= 1
if x in mp and mp[x] != 0:
print(f"{x} exists between [{l}, {r}]")
else:
print(f"{x} does not exist between [{l}, {r}]")
if __name__ == '__main__':
a = [1, 1, 5, 4, 5]
n = len(a)
q = [(0, 2, 2), (1, 4, 1), (2, 4, 5)]
m = len(q)
query_results(a, n, q, m)
|
C#
using System;
using System.Collections.Generic;
class Query {
public int L;
public int R;
public int x;
public Query(int L, int R, int x)
{
this.L = L;
this.R = R;
this.x = x;
}
}
class MainClass {
static void queryResults(int[] a, int n, List<Query> q,
int m)
{
int block = (int)Math.Sqrt(n);
q.Sort((x, y) => {
if (x.L / block != y.L / block) {
return x.L / block - y.L / block;
}
return x.R - y.R;
});
int currL = 0, currR = -1;
Dictionary<int, int> mp
= new Dictionary<int, int>();
for (int i = 0; i < m; i++)
{
int L = q[i].L, R = q[i].R, X = q[i].x;
while (currL > L)
{
currL--;
AddElement(mp, a[currL]);
}
while (currR < R)
{
currR++;
AddElement(mp, a[currR]);
}
while (currL < L) {
RemoveElement(mp, a[currL]);
currL++;
}
while (currR > R) {
RemoveElement(mp, a[currR]);
currR--;
}
if (mp.ContainsKey(X)) {
Console.WriteLine(X + " exists between ["
+ L + ", " + R + "]");
}
else {
Console.WriteLine(
X + " does not exist between [" + L
+ ", " + R + "]");
}
}
}
static void AddElement(Dictionary<int, int> mp, int key)
{
if (mp.ContainsKey(key)) {
mp[key]++;
}
else {
mp[key] = 1;
}
}
static void RemoveElement(Dictionary<int, int> mp,
int key)
{
if (mp.ContainsKey(key)) {
mp[key]--;
if (mp[key] == 0) {
mp.Remove(key);
}
}
}
public static void Main()
{
List<Query> q = new List<Query>();
q.Add(new Query(0, 2, 2));
q.Add(new Query(1, 4, 1));
q.Add(new Query(2, 4, 5));
int[] a = { 1, 1, 5, 4, 5 };
queryResults(a, a.Length, q, q.Count);
}
}
|
Javascript
let block;
class Query {
constructor(L, R, X) {
this.L = L;
this.R = R;
this.X = X;
}
}
function compare(x, y) {
if (Math.floor(x.L / block) !== Math.floor(y.L / block)) {
return Math.floor(x.L / block) - Math.floor(y.L / block);
}
return x.R - y.R;
}
function queryResults(a, n, q, m) {
block = Math.floor(Math.sqrt(n));
q.sort(compare);
let currL = 0;
let currR = 0;
const mp = new Map();
for (let i = 0; i < m; i++) {
const {
L,
R,
X
} = q[i];
while (currL < L) {
const value = mp.get(a[currL]);
if (value === 1) {
mp.delete(a[currL]);
} else {
mp.set(a[currL], value - 1);
}
currL++;
}
while (currL > L) {
currL--;
const value = mp.get(a[currL]);
mp.set(a[currL], value ? value + 1 : 1);
}
while (currR <= R) {
const value = mp.get(a[currR]);
mp.set(a[currR], value ? value + 1 : 1);
currR++;
}
while (currR > R + 1) {
currR--;
const value = mp.get(a[currR]);
if (value) {
mp.set(a[currR], value - 1);
}
}
if (mp.get(X) !== undefined && mp.get(X) > 0)
console.log(`${X} exists between [${L}, ${R}]`);
else
console.log(`${X} does not exist between [${L}, ${R}]`);
}
}
const a = [1, 1, 5, 4, 5];
const n = a.length;
let q = [new Query(0, 2, 2), new Query(1, 4, 1), new Query(2, 4, 5)];
let m = q.length;
queryResults(a, n, q, m);
|
Output2 does not exist between [0, 2]
1 exists between [1, 4]
5 exists between [2, 4]
Share your thoughts in the comments
Please Login to comment...