Area of a Regular Pentagram
Last Updated :
01 Sep, 2022
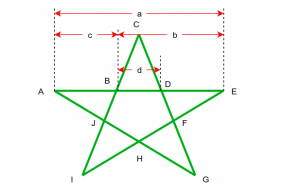
Given a Pentagram and its inner side length(d). The task is to find out the area of Pentagram. The Pentagram is a five-pointed star that is formed by drawing a continuous line in five straight segments.
Examples:
Input: d = 5
Output: Area = 139.187
Area of regular pentagram = 139.187
Input: d = 7
Output: Area = 272.807
Idea is to use Golden Ratio between a/b, b/c, and c/d which equals approximately 1.618
Inner side length d is given so
c = 1.618 * d
b = 1.618 * c
a = 1.618 * b
AB, BC and CD are equal(both side of regular pentagram)
So AB = BC = CD = c and BD is given by d.
Area of pentagram = Area of Pentagon BDFHJ + 5 * (Area of triangle BCD)
Area of Pentagon BDFHJ = (d2 * 5)/ (4* tan 36)
Area of triangle BCD = [s(s-d)(s-c)(s-c)]1/2 {Heron’s Formula}
where
s = (d + c + c)/2
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define PI 3.14159
using namespace std;
double areaOfTriangle(float d)
{
float c = 1.618 * d;
float s = (d + c + c) / 2;
double area = sqrt(s * (s - c) * (s - c) * (s - d));
return 5 * area;
}
double areaOfRegPentagon(float d)
{
double cal = 4 * tan(PI / 5);
double area = (5 * d * d) / cal;
return area;
}
double areaOfPentagram(float d)
{
return areaOfRegPentagon(d) + areaOfTriangle(d);
}
int main()
{
float d = 5;
cout << areaOfPentagram(d) << endl;
return 0;
}
|
Java
public class GFG {
static double PI = 3.14159;
static double areaOfTriangle(float d)
{
float c = (float)(1.618 * d);
float s = (d + c + c) / 2;
double area
= Math.sqrt(s * (s - c) * (s - c) * (s - d));
return 5 * area;
}
static double areaOfRegPentagon(float d)
{
double cal = 4 * Math.tan(PI / 5);
double area = (5 * d * d) / cal;
return area;
}
static double areaOfPentagram(float d)
{
return areaOfRegPentagon(d) + areaOfTriangle(d);
}
public static void main(String[] args)
{
float d = 5;
System.out.println(areaOfPentagram(d));
}
}
|
Python3
import math
PI = 3.14159
def areaOfTriangle(d):
c = 1.618 * d
s = (d + c + c) / 2
area = math.sqrt(s * (s - c) *
(s - c) * (s - d))
return 5 * area
def areaOfRegPentagon(d):
global PI
cal = 4 * math.tan(PI / 5)
area = (5 * d * d) / cal
return area
def areaOfPentagram(d):
return areaOfRegPentagon(d) + areaOfTriangle(d)
d = 5
print(areaOfPentagram(d))
|
C#
using System;
class GFG {
static double PI = 3.14159;
static double areaOfTriangle(float d)
{
float c = (float)(1.618 * d);
float s = (d + c + c) / 2;
double area
= Math.Sqrt(s * (s - c) * (s - c) * (s - d));
return 5 * area;
}
static double areaOfRegPentagon(float d)
{
double cal = 4 * Math.Tan(PI / 5);
double area = (5 * d * d) / cal;
return area;
}
static double areaOfPentagram(float d)
{
return areaOfRegPentagon(d) + areaOfTriangle(d);
}
public static void Main()
{
float d = 5;
Console.WriteLine(areaOfPentagram(d));
}
}
|
Javascript
<script>
var PI = 3.14159
function areaOfTriangle(d)
{
var c = 1.618 * d;
var s = (d + c + c) / 2;
var area = Math.sqrt(s * (s - c) *
(s - c) * (s - d));
return 5 * area;
}
function areaOfRegPentagon( d)
{
var cal = 4 * Math.tan(PI / 5);
var area = (5 * d * d) / cal;
return area;
}
function areaOfPentagram(d)
{
return areaOfRegPentagon(d) +
areaOfTriangle(d);
}
var d = 5;
document.write(areaOfPentagram(d).toFixed(3));
</script>
|
Time Complexity : O(log(N)), for using in-built sqrt() function.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...