Add and Remove vertex in Adjacency Matrix representation of Graph

A graph is a presentation of a set of entities where some pairs of entities are linked by a connection. Interconnected entities are represented by points referred to as vertices, and the connections between the vertices are termed as edges. Formally, a graph is a pair of sets (V, E), where V is a collection of vertices, and E is a collection of edges joining a pair of vertices. 

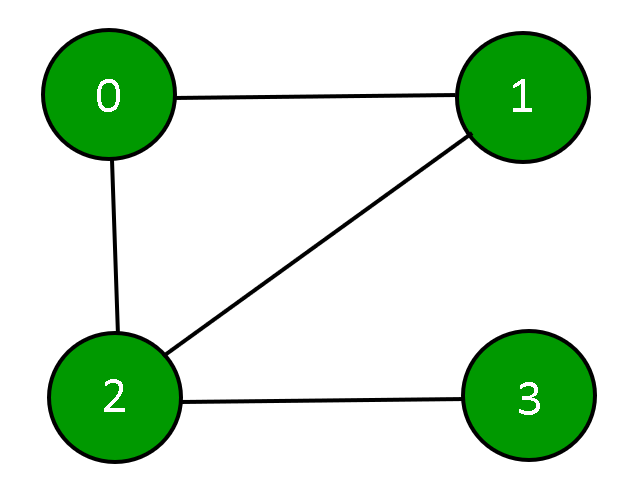
A graph can be represented by using an Adjacency Matrix.

Initialization of Graph: The adjacency matrix will be depicted using a 2D array, a constructor will be used to assign the size of the array and each element of that array will be initialized to 0. Showing that the degree of each vertex in the graph is zero.

C++

class Graph {
private:
    // number of vertices
    int n;

    // adjacency matrix
    int g[10][10];

public:
    // constructor
    Graph(int x)
    {
        n = x;

        // initializing each element of the adjacency matrix to zero
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                g[i][j] = 0;
            }
        }
    }
};

Java

class Graph {
    // number of vertices
    private int n;

    // adjacency matrix
    private int[][] g = new int[10][10];

    // constructor
    Graph(int x)
    {
        this.n = x;
        int i, j;

        // initializing each element of the adjacency matrix to zero
        for (i = 0; i < n; ++i) {
            for (j = 0; j < n; ++j) {
                g[i][j] = 0;
            }
        }
    }
}

Python3

class Graph:
     # number of vertices
     __n = 0

     # adjacency matrix
     __g =[[0 for x in range(10)] for y in range(10)]

     # constructor
     def __init__(self, x):
        self.__n = x

        # initializing each element of the adjacency matrix to zero
        for i in range(0, self.__n):
            for j in range(0, self.__n):
                self.__g[i][j]= 0

C#

class Graph{

// Number of vertices
private int n;

// Adjacency matrix
private int[,] g = new int[10, 10];

// Constructor
Graph(int x)
{
    this.n = x;
    int i, j;

    // Initializing each element of
    // the adjacency matrix to zero
    for(i = 0; i < n; ++i)
    {
        for(j = 0; j < n; ++j)
        {
            g[i, j] = 0;
        }
    }
}
}

// This code is contributed by ukasp

Javascript

class Graph {
    constructor(x) {
        // number of vertices
        this.n = x;

        // adjacency matrix
        this.g = [];

        // initializing each element of the adjacency matrix to zero
        for (let i = 0; i < this.n; ++i) {
            this.g[i] = [];
            for (let j = 0; j < this.n; ++j) {
                this.g[i][j] = 0;
            }
        }
    }
}

Here the adjacency matrix is g[n][n] in which the degree of each vertex is zero.

Displaying the Graph: The graph is depicted using the adjacency matrix g[n][n] having the number of vertices n. The 2D array(adjacency matrix) is displayed in which if there is an edge between two vertices ‘x’ and ‘y’ then g[x][y] is 1 otherwise 0.  

C++

void displayAdjacencyMatrix()
{
    cout << "\n\n Adjacency Matrix:";

    // displaying the 2D array
    for (int i = 0; i < n; ++i) {
        cout << "\n";
        for (int j = 0; j < n; ++j) {
            cout << " " << g[i][j];
        }
    }
}

Java

public void displayAdjacencyMatrix()
{
    System.out.print("\n\n Adjacency Matrix:");

    // displaying the 2D array
    for (int i = 0; i < n; ++i) {
        System.out.println();
        for (int j = 0; j < n; ++j) {
            System.out.print(" " + g[i][j]);
        }
    }
}

Python3

def displayAdjacencyMatrix(self):
        print("\n\n Adjacency Matrix:", end ="")

        # displaying the 2D array
        for i in range(0, self.__n):
            print()
            for j in range(0, self.__n):
                print("", self.__g[i][j], end ="")

C#

public void DisplayAdjacencyMatrix()
{
    Console.Write("\n\n Adjacency Matrix:");

    // Displaying the 2D array
    for (int i = 0; i < n; ++i)
    {
        Console.WriteLine();
        for (int j = 0; j < n; ++j)
        {
            Console.Write(" " + g[i,j]);
        }
    }
}

Javascript

function displayAdjacencyMatrix() {
    console.log("\n\n Adjacency Matrix:");

    // displaying the 2D array
    for (let i = 0; i < n; ++i) {
        let row = "";
        for (let j = 0; j < n; ++j) {
            row += " " + g[i][j];
        }
        console.log(row);
    }
}

The above method is a public member function of the class Graph which displays the graph using an adjacency matrix.

Adding Edges between Vertices in the Graph: To add edges between two existing vertices such as vertex ‘x’ and vertex ‘y’ then the elements g[x][y] and g[y][x] of the adjacency matrix will be assigned to 1, depicting that there is an edge between vertex ‘x’ and vertex ‘y’. 

C++

void addEdge(int x, int y)
{

    // checks if the vertex exists in the graph
    if ((x >= n) || (y > n)) {
        cout << "Vertex does not exists!";
    }

    // checks if the vertex is connecting to itself
    if (x == y) {
        cout << "Same Vertex!";
    }
    else {
        // connecting the vertices
        g[y][x] = 1;
        g[x][y] = 1;
    }
}

Java

public void addEdge(int x, int y)
{
    // checks if the vertex exists in the graph
    if ((x >= n) || (y > n)) {
        System.out.println("Vertex does not exists!");
    }

    // checks if the vertex is connecting to itself
    if (x == y) {
        System.out.println("Same Vertex!");
    }
    else {
        // connecting the vertices
        g[y][x] = 1;
        g[x][y] = 1;
    }
}

Python3

def addEdge(self, x, y):

        # checks if the vertex exists in the graph
        if(x>= self.__n) or (y >= self.__n):
            print("Vertex does not exists !")

        # checks if the vertex is connecting to itself
        if(x == y):
             print("Same Vertex !")
        else:

             # connecting the vertices
             self.__g[y][x]= 1
             self.__g[x][y]= 1

C#

public void AddEdge(int x, int y)
{
  // checks if the vertex exists in the graph
  if ((x >= n) || (y > n))
  {
    Console.WriteLine("Vertex does not exists!");
  }

  // checks if the vertex is connecting to itself
  if (x == y)
  {
    Console.WriteLine("Same Vertex!");
  }
  else
  {
    // connecting the vertices
    g[y, x] = 1;
    g[x, y] = 1;
  }
}

Javascript

function addEdge(x, y) {

    // checks if the vertex exists in the graph
    if ((x >= n) || (y > n)) {
        console.log("Vertex does not exist!");
    }

    // checks if the vertex is connecting to itself
    if (x === y) {
        console.log("Same Vertex!");
    }
    else {
        // connecting the vertices
        g[y][x] = 1;
        g[x][y] = 1;
    }
}

Here the above method is a public member function of the class Graph which connects any two existing vertices in the Graph.

Adding a Vertex in the Graph: To add a vertex in the graph, we need to increase both the row and column of the existing adjacency matrix and then initialize the new elements related to that vertex to 0.(i.e the new vertex added is not connected to any other vertex) 

C++

void addVertex()
{
    // increasing the number of vertices
    n++;
    int i;

    // initializing the new elements to 0
    for (i = 0; i < n; ++i) {
        g[i][n - 1] = 0;
        g[n - 1][i] = 0;
    }
}

Java

public void addVertex()
{
    // increasing the number of vertices
    n++;
    int i;

    // initializing the new elements to 0
    for (i = 0; i < n; ++i) {
        g[i][n - 1] = 0;
        g[n - 1][i] = 0;
    }
}

Python3

def addVertex(self):

         # increasing the number of vertices
         self.__n = self.__n + 1;

         # initializing the new elements to 0
         for i in range(0, self.__n):
             self.__g[i][self.__n-1]= 0
             self.__g[self.__n-1][i]= 0

Javascript

function addVertex() {
  // increasing the number of vertices
  n++;
  let i;

  // initializing the new elements to 0
  for (i = 0; i < n; ++i) {
    g[i][n - 1] = 0;
    g[n - 1][i] = 0;
  }
}

C#

public void addVertex()
{
    // increasing the number of vertices
    n++;
    int i;

    // initializing the new elements to 0
    for (i = 0; i < n; ++i) {
        g[i, n - 1] = 0;
        g[n - 1, i] = 0;
    }
}

The above method is a public member function of the class Graph which increments the number of vertices by 1 and the degree of the new vertex is 0.

Removing a Vertex in the Graph: To remove a vertex from the graph, we need to check if that vertex exists in the graph or not and if that vertex exists then we need to shift the rows to the left and the columns upwards of the adjacency matrix so that the row and column values of the given vertex gets replaced by the values of the next vertex and then decrease the number of vertices by 1.In this way that particular vertex will be removed from the adjacency matrix. 

C++

void removeVertex(int x)
{
    // checking if the vertex is present
    if (x > n) {
        cout << "\nVertex not present!";
        return;
    }
    else {
        int i;

        // removing the vertex
        while (x < n) {
            // shifting the rows to left side
            for (i = 0; i < n; ++i) {
                g[i][x] = g[i][x + 1];
            }

            // shifting the columns upwards
            for (i = 0; i < n; ++i) {
                g[x][i] = g[x + 1][i];
            }
            x++;
        }

        // decreasing the number of vertices
        n--;
    }
}

Java

public void removeVertex(int x)
{
    // checking if the vertex is present
    if (x > n) {
        System.out.println("Vertex not present!");
        return;
    }
    else {
        int i;

        // removing the vertex
        while (x < n) {

            // shifting the rows to left side
            for (i = 0; i < n; ++i) {
                g[i][x] = g[i][x + 1];
            }

            // shifting the columns upwards
            for (i = 0; i < n; ++i) {
                g[x][i] = g[x + 1][i];
            }
            x++;
        }

        // decreasing the number of vertices
        n--;
    }
}

Python3

def removeVertex(self, x):

        # checking if the vertex is present
        if(x>self.__n):
            print("Vertex not present !")
        else:

          # removing the vertex
          while(x<self.__n):

             # shifting the rows to left side
             for i in range(0, self.__n):
                  self.__g[i][x]= self.__g[i][x + 1]

             # shifting the columns upwards
             for i in range(0, self.__n):
                  self.__g[x][i]= self.__g[x + 1][i]
             x = x + 1

          # decreasing the number of vertices
          self.__n = self.__n - 1

C#

public void RemoveVertex(int x)
{
    // checking if the vertex is present
    if (x > n) {
        Console.WriteLine("Vertex not present!");
        return;
    }
    else {
        int i;

        // removing the vertex
        while (x < n) {

            // shifting the rows to left side
            for (i = 0; i < n; ++i) {
                g[i][x] = g[i][x + 1];
            }

            // shifting the columns upwards
            for (i = 0; i < n; ++i) {
                g[x][i] = g[x + 1][i];
            }
            x++;
        }

        // decreasing the number of vertices
        n--;
    }
}

Javascript

function removeVertex(x) {
  // checking if the vertex is present
  if (x > n) {
    console.log("\nVertex not present!");
    return;
  } else {
    let i;

    // removing the vertex
    while (x < n) {
      // shifting the rows to left side
      for (i = 0; i < n; ++i) {
        g[i][x] = g[i][x + 1];
      }

      // shifting the columns upwards
      for (i = 0; i < n; ++i) {
        g[x][i] = g[x + 1][i];
      }
      x++;
    }

    // decreasing the number of vertices
    n--;
  }
}

The above method is a public member function of the class Graph which removes an existing vertex from the graph by shifting the rows to the left and shifting the columns up to replace the row and column values of that vertex with the next vertex and then decreases the number of vertices by 1 in the graph.

Following is a complete program that uses all of the above methods in a Graph.

C++

// C++ program to add and remove Vertex in Adjacency Matrix

#include <iostream>

using namespace std;

class Graph {
private:
    // number of vertices
    int n;

    // adjacency matrix
    int g[10][10];

public:
    // constructor
    Graph(int x)
    {
        n = x;

        // initializing each element of the adjacency matrix to zero
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                g[i][j] = 0;
            }
        }
    }

    void displayAdjacencyMatrix()
    {
        cout << "\n\n Adjacency Matrix:";

        // displaying the 2D array
        for (int i = 0; i < n; ++i) {
            cout << "\n";
            for (int j = 0; j < n; ++j) {
                cout << " " << g[i][j];
            }
        }
    }

    void addEdge(int x, int y)
    {

        // checks if the vertex exists in the graph
        if ((x >= n) || (y > n)) {
            cout << "Vertex does not exists!";
        }

        // checks if the vertex is connecting to itself
        if (x == y) {
            cout << "Same Vertex!";
        }
        else {
            // connecting the vertices
            g[y][x] = 1;
            g[x][y] = 1;
        }
    }

    void addVertex()
    {
        // increasing the number of vertices
        n++;
        int i;

        // initializing the new elements to 0
        for (i = 0; i < n; ++i) {
            g[i][n - 1] = 0;
            g[n - 1][i] = 0;
        }
    }

    void removeVertex(int x)
    {
        // checking if the vertex is present
        if (x > n) {
            cout << "\nVertex not present!";
            return;
        }
        else {
            int i;

            // removing the vertex
            while (x < n) {
                // shifting the rows to left side
                for (i = 0; i < n; ++i) {
                    g[i][x] = g[i][x + 1];
                }

                // shifting the columns upwards
                for (i = 0; i < n; ++i) {
                    g[x][i] = g[x + 1][i];
                }
                x++;
            }

            // decreasing the number of vertices
            n--;
        }
    }
};

int main()
{
    // creating objects of class Graph
    Graph obj(4);

    // calling methods
    obj.addEdge(0, 1);
    obj.addEdge(0, 2);
    obj.addEdge(1, 2);
    obj.addEdge(2, 3);
    // the adjacency matrix created
    obj.displayAdjacencyMatrix();

    // adding a vertex to the graph
    obj.addVertex();
    // connecting that vertex to other existing vertices
    obj.addEdge(4, 1);
    obj.addEdge(4, 3);
    // the adjacency matrix with a new vertex
    obj.displayAdjacencyMatrix();

    // removing an existing vertex in the graph
    obj.removeVertex(1);
    // the adjacency matrix after removing a vertex
    obj.displayAdjacencyMatrix();

    return 0;
}

Java

// Java program to add and remove Vertex in Adjacency Matrix
class Graph
{
    // number of vertices
    private int n;

    // adjacency matrix
    private int[][] g = new int[10][10];

    // constructor
    Graph(int x)
    {
        this.n = x;
        int i, j;

        // initializing each element of
        // the adjacency matrix to zero
        for (i = 0; i < n; ++i)
        {
            for (j = 0; j < n; ++j)
            {
                g[i][j] = 0;
            }
        }
    }

    public void displayAdjacencyMatrix()
    {
        System.out.print("\n\n Adjacency Matrix:");

        // displaying the 2D array
        for (int i = 0; i < n; ++i)
        {
            System.out.println();
            for (int j = 0; j < n; ++j)
            {
                System.out.print(" " + g[i][j]);
            }
        }
    }

    public void addEdge(int x, int y)
    {
        // checks if the vertex exists in the graph
        if ((x >= n) || (y > n))
        {
            System.out.println("Vertex does not exists!");
        }

        // checks if the vertex is connecting to itself
        if (x == y)
        {
            System.out.println("Same Vertex!");
        }
        else
        {
            // connecting the vertices
            g[y][x] = 1;
            g[x][y] = 1;
        }
    }

    public void addVertex()
    {
        // increasing the number of vertices
        n++;
        int i;

        // initializing the new elements to 0
        for (i = 0; i < n; ++i)
        {
            g[i][n - 1] = 0;
            g[n - 1][i] = 0;
        }
    }

    public void removeVertex(int x)
    {
        // checking if the vertex is present
        if (x > n)
        {
            System.out.println("Vertex not present!");
            return;
        }
        else
        {
            int i;

            // removing the vertex
            while (x < n)
            {

                // shifting the rows to left side
                for (i = 0; i < n; ++i)
                {
                    g[i][x] = g[i][x + 1];
                }

                // shifting the columns upwards
                for (i = 0; i < n; ++i)
                {
                    g[x][i] = g[x + 1][i];
                }
                x++;
            }

            // decreasing the number of vertices
            n--;
        }
    }
}

class Main
{
    public static void main(String[] args)
    {
        // creating objects of class Graph
        Graph obj = new Graph(4);

        // calling methods
        obj.addEdge(0, 1);
        obj.addEdge(0, 2);
        obj.addEdge(1, 2);
        obj.addEdge(2, 3);

        // the adjacency matrix created
        obj.displayAdjacencyMatrix();

        // adding a vertex to the graph
        obj.addVertex();

        // connecting that vertex to other existing vertices
        obj.addEdge(4, 1);
        obj.addEdge(4, 3);

        // the adjacency matrix with a new vertex
        obj.displayAdjacencyMatrix();

        // removing an existing vertex in the graph
        obj.removeVertex(1);

        // the adjacency matrix after removing a vertex
        obj.displayAdjacencyMatrix();
    }
}

Python3

# Python program to add and remove Vertex in Adjacency Matrix

class Graph:
     # number of vertices
     __n = 0

     # adjacency matrix
     __g =[[0 for x in range(10)] for y in range(10)]

     # constructor
     def __init__(self, x):
        self.__n = x

        # initializing each element of the adjacency matrix to zero
        for i in range(0, self.__n):
            for j in range(0, self.__n):
                self.__g[i][j]= 0

     def displayAdjacencyMatrix(self):
        print("\n\n Adjacency Matrix:", end ="")

        # displaying the 2D array
        for i in range(0, self.__n):
            print()
            for j in range(0, self.__n):
                print("", self.__g[i][j], end ="")
     def addEdge(self, x, y):

        # checks if the vertex exists in the graph
        if(x>= self.__n) or (y >= self.__n):
            print("Vertex does not exists !")

        # checks if the vertex is connecting to itself
        if(x == y):
             print("Same Vertex !")
        else:

             # connecting the vertices
             self.__g[y][x]= 1
             self.__g[x][y]= 1

     def addVertex(self):

         # increasing the number of vertices
         self.__n = self.__n + 1;

         # initializing the new elements to 0
         for i in range(0, self.__n):
             self.__g[i][self.__n-1]= 0
             self.__g[self.__n-1][i]= 0
     def removeVertex(self, x):

        # checking if the vertex is present
        if(x>self.__n):
             print("Vertex not present !")
        else:

             # removing the vertex
             while(x<self.__n):

                 # shifting the rows to left side
                 for i in range(0, self.__n):
                       self.__g[i][x]= self.__g[i][x + 1]

                 # shifting the columns upwards
                 for i in range(0, self.__n):
                       self.__g[x][i]= self.__g[x + 1][i]
                 x = x + 1

             # decreasing the number of vertices
             self.__n = self.__n - 1


# creating objects of class Graph
obj = Graph(4);

# calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
# the adjacency matrix created
obj.displayAdjacencyMatrix();

# adding a vertex to the graph
obj.addVertex();
# connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
# the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();

# removing an existing vertex in the graph
obj.removeVertex(1);
# the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();

C#

// C# program to add and remove Vertex in Adjacency Matrix
using System;

public class Graph
{
    // number of vertices
    private int n;

    // adjacency matrix
    private int[,] g = new int[10, 10];

    // constructor
    public Graph(int x)
    {
        this.n = x;
        int i, j;

        // initializing each element of the adjacency matrix to zero
        for (i = 0; i < n; ++i)
        {
            for (j = 0; j < n; ++j)
            {
                g[i, j] = 0;
            }
        }
    }

    public void displayAdjacencyMatrix()
    {
        Console.Write("\n\n Adjacency Matrix:");

        // displaying the 2D array
        for (int i = 0; i < n; ++i)
        {
            Console.WriteLine();
            for (int j = 0; j < n; ++j)
            {
                Console.Write(" " + g[i, j]);
            }
        }
    }

    public void addEdge(int x, int y)
    {
        // checks if the vertex exists in the graph
        if ((x >= n) || (y > n))
        {
            Console.WriteLine("Vertex does not exists!");
        }

        // checks if the vertex is connecting to itself
        if (x == y)
        {
            Console.WriteLine("Same Vertex!");
        }
        else
        {
            // connecting the vertices
            g[y, x] = 1;
            g[x, y] = 1;
        }
    }

    public void addVertex()
    {
        // increasing the number of vertices
        n++;
        int i;

        // initializing the new elements to 0
        for (i = 0; i < n; ++i)
        {
            g[i, n - 1] = 0;
            g[n - 1, i] = 0;
        }
    }

    public void removeVertex(int x)
    {
        // checking if the vertex is present
        if (x > n)
        {
            Console.WriteLine("Vertex not present!");
            return;
        }
        else
        {
            int i;

            // removing the vertex
            while (x < n)
            {

                // shifting the rows to left side
                for (i = 0; i < n; ++i)
                {
                    g[i, x] = g[i, x + 1];
                }

                // shifting the columns upwards
                for (i = 0; i < n; ++i)
                {
                    g[x, i] = g[x + 1, i];
                }
                x++;
            }

            // decreasing the number of vertices
            n--;
        }
    }
}

public class GFG
{
    // Driver code
    public static void Main(String[] args)
    {
        // creating objects of class Graph
        Graph obj = new Graph(4);

        // calling methods
        obj.addEdge(0, 1);
        obj.addEdge(0, 2);
        obj.addEdge(1, 2);
        obj.addEdge(2, 3);
        // the adjacency matrix created
        obj.displayAdjacencyMatrix();

        // adding a vertex to the graph
        obj.addVertex();

        // connecting that vertex to other existing vertices
        obj.addEdge(4, 1);
        obj.addEdge(4, 3);

        // the adjacency matrix with a new vertex
        obj.displayAdjacencyMatrix();

        // removing an existing vertex in the graph
        obj.removeVertex(1);

        // the adjacency matrix after removing a vertex
        obj.displayAdjacencyMatrix();
    }
}

// This code is contributed by PrinciRaj1992

Javascript

<script>
// Javascript program to add and remove Vertex in Adjacency Matrix

class Graph
{

    // constructor
    constructor(x)
    {
        // number of vertices
        this.n=x;

        // adjacency matrix
        this.g = new Array(10);
        for(let i=0;i<10;i++)
        {
            this.g[i]=new Array(10);
            for(let j=0;j<10;j++)
            {
                this.g[i][j]=0;
            }
        }
    }

    displayAdjacencyMatrix()
    {
        document.write("<br><br> Adjacency Matrix:");

        // displaying the 2D array
        for (let i = 0; i < this.n; ++i)
        {
            document.write("<br>");
            for (let j = 0; j < this.n; ++j)
            {
                document.write(" " + this.g[i][j]);
            }
        }
    }

    addEdge(x,y)
    {
        // checks if the vertex exists in the graph
        if ((x >= this.n) || (y > this.n))
        {
            document.write("Vertex does not exists!<br>");
        }

        // checks if the vertex is connecting to itself
        if (x == y)
        {
            document.write("Same Vertex!<br>");
        }
        else
        {
            // connecting the vertices
            this.g[y][x] = 1;
            this.g[x][y] = 1;
        }
    }

    addVertex()
    {
        // increasing the number of vertices
        this.n++;
        let i;

        // initializing the new elements to 0
        for (i = 0; i < this.n; ++i)
        {
            this.g[i][this.n - 1] = 0;
            this.g[this.n - 1][i] = 0;
        }
    }

    removeVertex(x)
    {
        // checking if the vertex is present
        if (x > this.n)
        {
            document.write("Vertex not present!<br>");
            return;
        }
        else
        {
            let i;

            // removing the vertex
            while (x < this.n)
            {

                // shifting the rows to left side
                for (i = 0; i < this.n; ++i)
                {
                    this.g[i][x] = this.g[i][x + 1];
                }

                // shifting the columns upwards
                for (i = 0; i < this.n; ++i)
                {
                    this.g[x][i] = this.g[x + 1][i];
                }
                x++;
            }

            // decreasing the number of vertices
            this.n--;
        }
    }

}

// creating objects of class Graph
let obj = new Graph(4);

// calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);

// the adjacency matrix created
obj.displayAdjacencyMatrix();

// adding a vertex to the graph
obj.addVertex();

// connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);

// the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();

// removing an existing vertex in the graph
obj.removeVertex(1);

// the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();





// This code is contributed by rag2127
</script>

Output:

Adjacency Matrix:
0 1 1 0
1 0 1 0
1 1 0 1
0 0 1 0

Adjacency Matrix:
0 1 1 0 0
1 0 1 0 1
1 1 0 1 0
0 0 1 0 1
0 1 0 1 0

Adjacency Matrix:
0 1 0 0
1 0 1 0
0 1 0 1
0 0 1 0

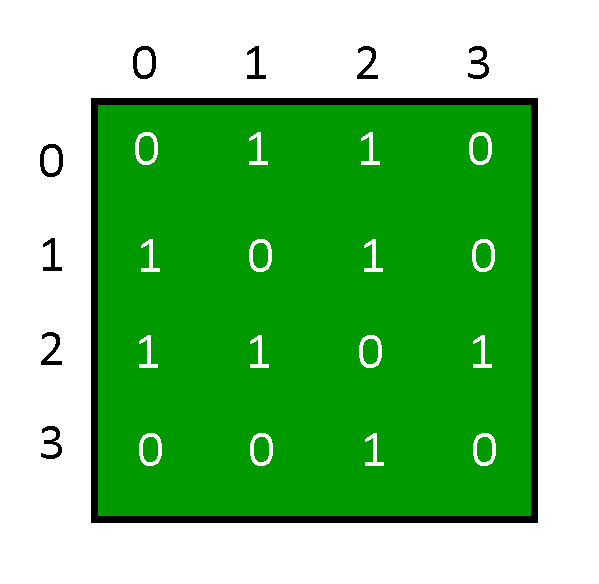
Adjacency matrices waste a lot of memory space. Such matrices are found to be very sparse. This representation requires space for n*n elements, the time complexity of the addVertex() method is O(n), and the time complexity of the removeVertex() method is O(n*n) for a graph of n vertices. 

From the output of the program, the Adjacency Matrix is:

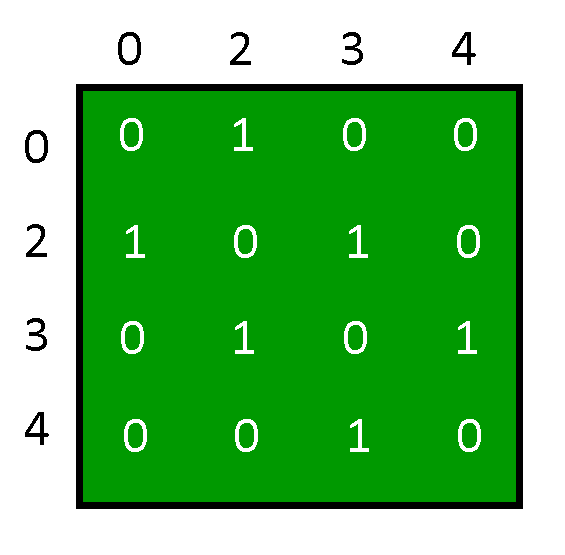
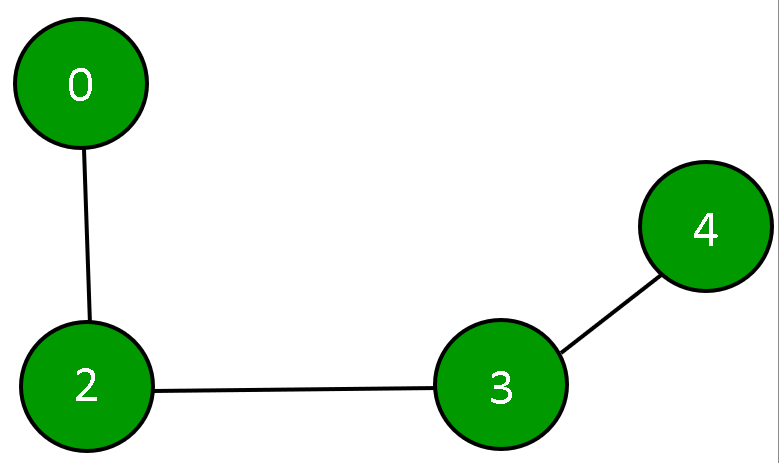
And the Graph depicted by the above Adjacency Matrix is: