Add and Remove Edge in Adjacency List representation of a Graph
Last Updated :
05 Mar, 2023
Prerequisites: Graph and Its Representation
In this article, adding and removing edge is discussed in a given adjacency list representation.
A vector has been used to implement the graph using adjacency list representation. It is used to store the adjacency lists of all the vertices. The vertex number is used as the index in this vector.
Example:
Below is a graph and its adjacency list representation:
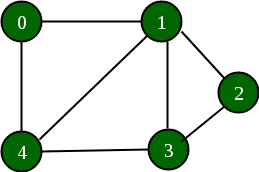
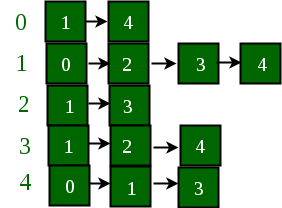
If the edge between 1 and 4 has to be removed, then the above graph and the adjacency list transforms to:
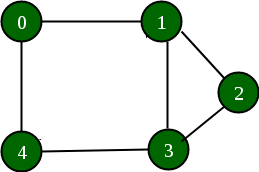
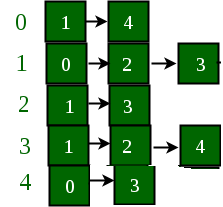
Approach: The idea is to represent the graph as an array of vectors such that every vector represents adjacency list of the vertex.
- Adding an edge: Adding an edge is done by inserting both of the vertices connected by that edge in each others list. For example, if an edge between (u, v) has to be added, then u is stored in v’s vector list and v is stored in u’s vector list. (push_back)
- Deleting an edge: To delete edge between (u, v), u’s adjacency list is traversed until v is found and it is removed from it. The same operation is performed for v.(erase)
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void delEdge(vector<int> adj[], int u, int v)
{
for (int i = 0; i < adj[u].size(); i++) {
if (adj[u][i] == v) {
adj[u].erase(adj[u].begin() + i);
break;
}
}
for (int i = 0; i < adj[v].size(); i++) {
if (adj[v][i] == u) {
adj[v].erase(adj[v].begin() + i);
break;
}
}
}
void printGraph(vector<int> adj[], int V)
{
for (int v = 0; v < V; ++v) {
cout << "vertex " << v << " ";
for (auto x : adj[v])
cout << "-> " << x;
printf("\n");
}
printf("\n");
}
int main()
{
int V = 5;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
delEdge(adj, 1, 4);
printGraph(adj, V);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void addEdge(Vector<Integer> adj[],
int u, int v)
{
adj[u].add(v);
adj[v].add(u);
}
static void delEdge(Vector<Integer> adj[],
int u, int v)
{
for (int i = 0; i < adj[u].size(); i++)
{
if (adj[u].get(i) == v)
{
adj[u].remove(i);
break;
}
}
for (int i = 0; i < adj[v].size(); i++)
{
if (adj[v].get(i) == u)
{
adj[v].remove(i);
break;
}
}
}
static void printGraph(Vector<Integer> adj[], int V)
{
for (int v = 0; v < V; ++v)
{
System.out.print("vertex " + v+ " ");
for (Integer x : adj[v])
System.out.print("-> " + x);
System.out.printf("\n");
}
System.out.printf("\n");
}
public static void main(String[] args)
{
int V = 5;
Vector<Integer> []adj = new Vector[V];
for (int i = 0; i < V; i++)
adj[i] = new Vector<Integer>();
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
delEdge(adj, 1, 4);
printGraph(adj, V);
}
}
|
Python3
def addEdge(adj, u, v):
adj[u].append(v);
adj[v].append(u);
def delEdge(adj, u, v):
for i in range(len(adj[u])):
if (adj[u][i] == v):
adj[u].pop(i);
break;
for i in range(len(adj[v])):
if (adj[v][i] == u):
adj[v].pop(i);
break;
def prGraph(adj, V):
for v in range(V):
print("vertex " + str(v), end = ' ')
for x in adj[v]:
print("-> " + str(x), end = '')
print()
print()
if __name__=='__main__':
V = 5;
adj = [[] for i in range(V)]
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
prGraph(adj, V);
delEdge(adj, 1, 4);
prGraph(adj, V);
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void addEdge(List<int> []adj,
int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static void delEdge(List<int> []adj,
int u, int v)
{
for (int i = 0; i < adj[u].Count; i++)
{
if (adj[u][i] == v)
{
adj[u].RemoveAt(i);
break;
}
}
for (int i = 0; i < adj[v].Count; i++)
{
if (adj[v][i] == u)
{
adj[v].RemoveAt(i);
break;
}
}
}
static void printGraph(List<int> []adj, int V)
{
for (int v = 0; v < V; ++v)
{
Console.Write("vertex " + v + " ");
foreach (int x in adj[v])
Console.Write("-> " + x);
Console.Write("\n");
}
Console.Write("\n");
}
public static void Main(String[] args)
{
int V = 5;
List<int> []adj = new List<int>[V];
for (int i = 0; i < V; i++)
adj[i] = new List<int>();
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
delEdge(adj, 1, 4);
printGraph(adj, V);
}
}
|
Javascript
const addEdge = (adj, u, v) => {
adj[u].push(v);
adj[v].push(u);
};
const delEdge = (adj, u, v) => {
const indexOfVInU = adj[u].indexOf(v);
adj[u].splice(indexOfVInU, 1);
const indexOfUInV = adj[v].indexOf(u);
adj[v].splice(indexOfUInV, 1);
};
const printGraph = (adj, V) => {
for (let v = 0; v < V; v++) {
console.log(`vertex ${v} `, adj[v].join("-> "));
}
};
const main = () => {
const V = 5;
const adj = [];
for (let i = 0; i < V; i++) {
adj[i] = [];
}
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
delEdge(adj, 1, 4);
printGraph(adj, V);
};
main();
|
Output:
vertex 0 -> 1-> 4
vertex 1 -> 0-> 2-> 3-> 4
vertex 2 -> 1-> 3
vertex 3 -> 1-> 2-> 4
vertex 4 -> 0-> 1-> 3
vertex 0 -> 1-> 4
vertex 1 -> 0-> 2-> 3
vertex 2 -> 1-> 3
vertex 3 -> 1-> 2-> 4
vertex 4 -> 0-> 3
Time Complexity: Removing an edge from adjacent list requires, on the average time complexity will be O(|E| / |V|) , which may result in cubical complexity for dense graphs to remove all edges.
Auxiliary Space: O(V) , here V is number of vertices.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...