Absolute difference between sum and product of roots of a quartic equation
Last Updated :
20 Aug, 2022
Given a quartic equation in the form 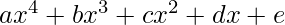 , determine the absolute difference between the sum of its roots and the product of its roots. Note that roots need not be real – they can also be complex.
, determine the absolute difference between the sum of its roots and the product of its roots. Note that roots need not be real – they can also be complex.
Examples:
Input: 4x^4 + 3x^3 + 2x^2 + x - 1
Output: 0.5
Input: x^4 + 4x^3 + 6x^2 + 4x + 1
Output: 5
Approach: Solving the quartic equation to obtain each individual root would be time-consuming and inefficient, and would require much effort and computational power. A more efficient solution utilises the following formulae:
The quartic 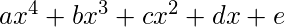 always has sum of roots
always has sum of roots 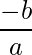 ,and product of roots
,and product of roots  .
.
Hence by computing 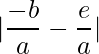 we find the absolute difference between sum and product of roots.
we find the absolute difference between sum and product of roots.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double sumProductDifference(int a, int b,
int c, int d,
int e)
{
double rootSum = (double)(-1 * b) / a;
double rootProduct = (double) e / a;
return abs(rootSum - rootProduct);
}
int main()
{
cout << sumProductDifference(8, 4, 6, 4, 1);
return 0;
}
|
Java
public class GFG {
static double sumProductDifference(int a, int b, int c, int d, int e) {
double rootSum = (double)(-1 * b) / a;
double rootProduct = (double) e / a;
return Math.abs(rootSum - rootProduct);
}
public static void main(String args[]) {
System.out.println(sumProductDifference(8, 4, 6, 4, 1));
}
}
|
Python3
def sumProductDifference(a, b, c, d, e):
rootSum = (-1 * b)/a
rootProduct = e / a
return abs(rootSum-rootProduct)
print(sumProductDifference(8, 4, 6, 4, 1))
|
C#
using System;
class GFG
{
static double sumProductDifference(int a, int b,
int c, int d,
int e)
{
double rootSum = (double)(-1 * b) / a;
double rootProduct = (double) e / a;
return Math.Abs(rootSum - rootProduct);
}
public static void Main()
{
Console.Write(sumProductDifference(8, 4, 6, 4, 1));
}
}
|
PHP
<?php
function sumProductDifference($a, $b,
$c, $d,$e)
{
$rootSum = (double)(-1 * $b) / $a;
$rootProduct = (double) $e / $a;
return abs($rootSum - $rootProduct);
}
echo sumProductDifference(8, 4, 6, 4, 1);
?>
|
Javascript
<script>
function sumProductDifference(a, b, c, d, e)
{
var rootSum = (-1 * b) / a;
var rootProduct = e / a;
return Math.abs(rootSum - rootProduct);
}
document.write(sumProductDifference(8, 4, 6, 4, 1));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Explanation: The input equation is 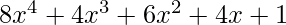 .
.
By finding 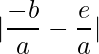 , we get
, we get 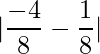 ,
,
which is  , or
, or 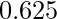 .
.
Share your thoughts in the comments
Please Login to comment...