Print nodes between two given level numbers of a binary tree
Last Updated :
12 Jan, 2023
Given a binary tree and two level numbers ‘low’ and ‘high’, print nodes from level low to level high.
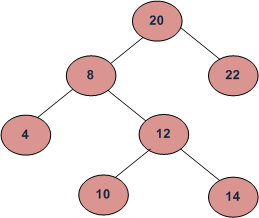
For example consider the binary tree given in below diagram.
Input: Root of below tree, low = 2, high = 4
Output:
8 22
4 12
10 14
A Simple Method is to first write a recursive function that prints nodes of a given level number. Then call a recursive function in a loop from low to high. Time complexity of this method is O(n2)
We can print nodes in O(n) time using queue-based iterative level order traversal. The idea is to do simple queue-based level order traversal. While doing inorder traversal, add a marker node at the end. Whenever we see a marker node, we increase level number. If level number is between low and high, then print nodes.
The following is the implementation of above idea.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int key;
struct Node* left, *right;
};
void printLevels(Node* root, int low, int high)
{
queue <Node *> Q;
Node *marker = new Node;
int level = 1;
Q.push(root);
Q.push(marker);
while (Q.empty() == false)
{
Node *n = Q.front();
Q.pop();
if (n == marker)
{
cout << endl;
level++;
if (Q.empty() == true || level > high) break;
Q.push(marker);
continue;
}
if (level >= low)
cout << n->key << " ";
if (n->left != NULL) Q.push(n->left);
if (n->right != NULL) Q.push(n->right);
}
}
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return (temp);
}
int main()
{
struct Node *root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
cout << "Level Order traversal between given two levels is";
printLevels(root, 2, 3);
return 0;
}
|
Java
import java.util.LinkedList;
import java.util.Queue;
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree
{
Node root;
void printLevels(Node node, int low, int high)
{
Queue<Node> Q = new LinkedList<>();
Node marker = new Node(4);
int level = 1;
Q.add(node);
Q.add(marker);
while (Q.isEmpty() == false)
{
Node n = Q.peek();
Q.remove();
if (n == marker)
{
System.out.println("");
level++;
if (Q.isEmpty() == true || level > high)
break;
Q.add(marker);
continue;
}
if (level >= low)
System.out.print( n.data + " ");
if (n.left != null)
Q.add(n.left);
if (n.right != null)
Q.add(n.right);
}
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
System.out.print("Level Order traversal between given two levels is ");
tree.printLevels(tree.root, 2, 3);
}
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def printLevels(root, low, high):
Q = []
marker = Node(11114)
level = 1
Q.append(root)
Q.append(marker)
while(len(Q) >0):
n = Q[0]
Q.pop(0)
if n == marker:
print()
level += 1
if len(Q) == 0 or level > high:
break
Q.append(marker)
continue
if level >= low:
print (n.key,end=" ")
if n.left is not None:
Q.append(n.left)
Q.append(n.right)
root = Node(20)
root.left = Node(8)
root.right = Node(22)
root.left.left = Node(4)
root.left.right = Node(12)
root.left.right.left = Node(10)
root.left.right.right = Node(14)
print ("Level Order Traversal between given two levels is",printLevels(root,2,3))
|
C#
using System;
using System.Collections.Generic;
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
public Node root;
public virtual void printLevels(Node node, int low, int high)
{
LinkedList<Node> Q = new LinkedList<Node>();
Node marker = new Node(4);
int level = 1;
Q.AddLast(node);
Q.AddLast(marker);
while (Q.Count > 0)
{
Node n = Q.First.Value;
Q.RemoveFirst();
if (n == marker)
{
Console.WriteLine("");
level++;
if (Q.Count == 0 || level > high)
{
break;
}
Q.AddLast(marker);
continue;
}
if (level >= low)
{
Console.Write(n.data + " ");
}
if (n.left != null)
{
Q.AddLast(n.left);
}
if (n.right != null)
{
Q.AddLast(n.right);
}
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
Console.Write("Level Order traversal between given two levels is ");
tree.printLevels(tree.root, 2, 3);
}
}
|
Javascript
<script>
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
var root = null;
function printLevels(node, low, high)
{
var Q = [];
var marker = new Node(4);
var level = 1;
Q.push(node);
Q.push(marker);
while (Q.length > 0)
{
var n = Q[0];
Q.shift();
if (n == marker)
{
document.write("<br>");
level++;
if (Q.length == 0 || level > high)
{
break;
}
Q.push(marker);
continue;
}
if (level >= low)
{
document.write(n.data + " ");
}
if (n.left != null)
{
Q.push(n.left);
}
if (n.right != null)
{
Q.push(n.right);
}
}
}
root = new Node(20);
root.left = new Node(8);
root.right = new Node(22);
root.left.left = new Node(4);
root.left.right = new Node(12);
root.left.right.left = new Node(10);
root.left.right.right = new Node(14);
document.write("Level Order traversal between given two levels is ");
printLevels(root, 2, 3);
</script>
|
Output
Level Order traversal between given two levels is
8 22
4 12
Time complexity of above method is O(n) as it does a simple level order traversal.
Auxiliary Space: O(N) where N is the number of nodes in the binary tree due to queue.
Share your thoughts in the comments
Please Login to comment...