Subset Sum Problem
Last Updated :
23 Apr, 2024
Given a set of non-negative integers and a value sum, the task is to check if there is a subset of the given set whose sum is equal to the given sum.
Examples:
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True
Explanation: There is a subset (4, 5) with sum 9.
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30
Output: False
Explanation: There is no subset that add up to 30.
Subset Sum Problem using Recursion:
For the recursive approach, there will be two cases.
- Consider the ‘last’ element to be a part of the subset. Now the new required sum = required sum – value of ‘last’ element.
- Don’t include the ‘last’ element in the subset. Then the new required sum = old required sum.
In both cases, the number of available elements decreases by 1.
Mathematically the recurrence relation will look like the following:
isSubsetSum(set, n, sum) = isSubsetSum(set, n-1, sum) | isSubsetSum(set, n-1, sum-set[n-1])
Base Cases:
isSubsetSum(set, n, sum) = false, if sum > 0 and n = 0
isSubsetSum(set, n, sum) = true, if sum = 0
The structure of the recursion tree will be like the following:
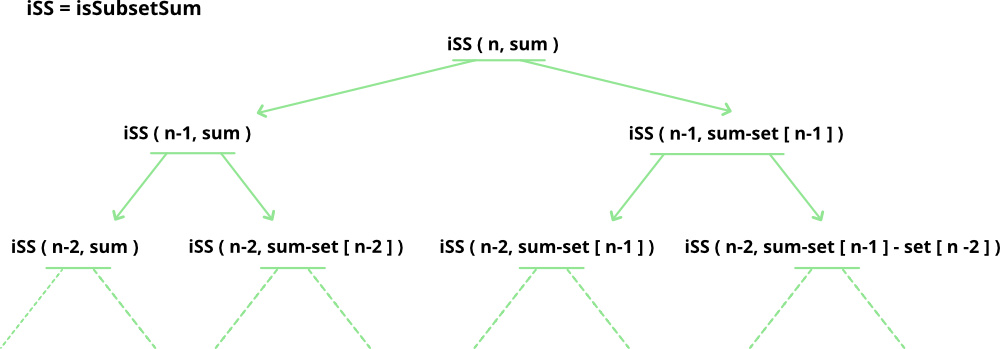
Structure of the recursion tree of the above recursion formula
Follow the below steps to implement the recursion:
- Build a recursive function and pass the index to be considered (here gradually moving from the last end) and the remaining sum amount.
- For each index check the base cases and utilize the above recursive call.
- If the answer is true for any recursion call, then there exists such a subset. Otherwise, no such subset exists.
Below is the implementation of the above approach.
C++
// A recursive solution for subset sum problem
#include <bits/stdc++.h>
using namespace std;
// Returns true if there is a subset
// of set[] with sum equal to given sum
bool isSubsetSum(int set[], int n, int sum)
{
// Base Cases
if (sum == 0)
return true;
if (n == 0)
return false;
// If last element is greater than sum,
// then ignore it
if (set[n - 1] > sum)
return isSubsetSum(set, n - 1, sum);
// Else, check if sum can be obtained by any
// of the following:
// (a) including the last element
// (b) excluding the last element
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// Driver code
int main()
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
cout << "Found a subset with given sum";
else
cout << "No subset with given sum";
return 0;
}
// This code is contributed by shivanisinghss2110
// A recursive solution for subset sum problem
#include <stdio.h>
#include <stdbool.h>
// Returns true if there is a subset
// of set[] with sum equal to given sum
bool isSubsetSum(int set[], int n, int sum)
{
// Base Cases
if (sum == 0)
return true;
if (n == 0)
return false;
// If last element is greater than sum,
// then ignore it
if (set[n - 1] > sum)
return isSubsetSum(set, n - 1, sum);
// Else, check if sum can be obtained by any
// of the following:
// (a) including the last element
// (b) excluding the last element
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// Driver code
int main()
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
printf("Found a subset with given sum");
else
printf("No subset with given sum");
return 0;
}
// A recursive solution for subset sum
import java.io.*;
class GFG {
// Returns true if there is a subset
// of set[] with sum equal to given sum
static boolean isSubsetSum(int set[], int n, int sum)
{
// Base Cases
if (sum == 0)
return true;
if (n == 0)
return false;
// If last element is greater than
// sum, then ignore it
if (set[n - 1] > sum)
return isSubsetSum(set, n - 1, sum);
// Else, check if sum can be obtained
// by any of the following
// (a) including the last element
// (b) excluding the last element
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// Driver code
public static void main(String args[])
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.length;
if (isSubsetSum(set, n, sum) == true)
System.out.println("Found a subset"
+ " with given sum");
else
System.out.println("No subset with"
+ " given sum");
}
}
/* This code is contributed by Rajat Mishra */
# A recursive solution for subset sum
# problem
# Returns true if there is a subset
# of set[] with sun equal to given sum
def isSubsetSum(set, n, sum):
# Base Cases
if (sum == 0):
return True
if (n == 0):
return False
# If last element is greater than
# sum, then ignore it
if (set[n - 1] > sum):
return isSubsetSum(set, n - 1, sum)
# Else, check if sum can be obtained
# by any of the following
# (a) including the last element
# (b) excluding the last element
return isSubsetSum(
set, n-1, sum) or isSubsetSum(
set, n-1, sum-set[n-1])
# Driver code
if __name__ == '__main__':
set = [3, 34, 4, 12, 5, 2]
sum = 9
n = len(set)
if (isSubsetSum(set, n, sum) == True):
print("Found a subset with given sum")
else:
print("No subset with given sum")
# This code is contributed by Nikita Tiwari.
// A recursive solution for subset sum problem
using System;
class GFG {
// Returns true if there is a subset of set[]
// with sum equal to given sum
static bool isSubsetSum(int[] set, int n, int sum)
{
// Base Cases
if (sum == 0)
return true;
if (n == 0)
return false;
// If last element is greater than sum,
// then ignore it
if (set[n - 1] > sum)
return isSubsetSum(set, n - 1, sum);
// Else, check if sum can be obtained
// by any of the following
// (a) including the last element
// (b) excluding the last element
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// Driver code
public static void Main()
{
int[] set = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.Length;
if (isSubsetSum(set, n, sum) == true)
Console.WriteLine(
"Found a subset with given sum");
else
Console.WriteLine("No subset with given sum");
}
}
// This code is contributed by Sam007
<script>
// A recursive solution for subset sum problem
// Returns true if there is a subset of set[] with sum
// equal to given sum
function isSubsetSum(set, n, sum)
{
// Base Cases
if (sum == 0)
return true;
if (n == 0)
return false;
// If last element is greater than sum,
// then ignore it
if (set[n - 1] > sum)
return isSubsetSum(set, n - 1, sum);
// Else, check if sum can be obtained
// by any of the following
// (a) including the last element
// (b) excluding the last element
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
let set = [ 3, 34, 4, 12, 5, 2 ];
let sum = 9;
let n = set.length;
if (isSubsetSum(set, n, sum) == true)
document.write("Found a subset with given sum");
else
document.write("No subset with given sum");
// This code is contributed by mukesh07.
</script>
<?php
// A recursive solution for subset sum problem
// Returns true if there is a subset of set
// with sun equal to given sum
function isSubsetSum($set, $n, $sum)
{
// Base Cases
if ($sum == 0)
return true;
if ($n == 0)
return false;
// If last element is greater
// than sum, then ignore it
if ($set[$n - 1] > $sum)
return isSubsetSum($set, $n - 1, $sum);
// Else, check if sum can be
// obtained by any of the following
// (a) including the last element
// (b) excluding the last element
return isSubsetSum($set, $n - 1, $sum) ||
isSubsetSum($set, $n - 1,
$sum - $set[$n - 1]);
}
// Driver Code
$set = array(3, 34, 4, 12, 5, 2);
$sum = 9;
$n = 6;
if (isSubsetSum($set, $n, $sum) == true)
echo"Found a subset with given sum";
else
echo "No subset with given sum";
// This code is contributed by Anuj_67
?>
OutputFound a subset with given sum
Complexity Analysis:
- Time Complexity: O(2n) The above solution may try all subsets of the given set in worst case. Therefore time complexity of the above solution is exponential. The problem is in-fact NP-Complete (There is no known polynomial time solution for this problem).
- Auxiliary Space: O(n) where n is recursion stack space.
Subset Sum Problem using Memoization:
As seen in the previous recursion method, each state of the solution can be uniquely identified using two variables – the index and the remaining sum. So create a 2D array to store the value of each state to avoid recalculation of the same state.
Below is the implementation of the above approach:
C++
// CPP program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Taking the matrix as globally
int tab[2000][2000];
// Check if possible subset with
// given sum is possible or not
int subsetSum(int a[], int n, int sum)
{
// If the sum is zero it means
// we got our expected sum
if (sum == 0)
return 1;
if (n <= 0)
return 0;
// If the value is not -1 it means it
// already call the function
// with the same value.
// it will save our from the repetition.
if (tab[n - 1][sum] != -1)
return tab[n - 1][sum];
// If the value of a[n-1] is
// greater than the sum.
// we call for the next value
if (a[n - 1] > sum)
return tab[n - 1][sum] = subsetSum(a, n - 1, sum);
else
{
// Here we do two calls because we
// don't know which value is
// full-fill our criteria
// that's why we doing two calls
return tab[n - 1][sum] = subsetSum(a, n - 1, sum) ||
subsetSum(a, n - 1, sum - a[n - 1]);
}
}
// Driver Code
int main()
{
// Storing the value -1 to the matrix
memset(tab, -1, sizeof(tab));
int n = 5;
int a[] = {1, 5, 3, 7, 4};
int sum = 12;
if (subsetSum(a, n, sum))
{
cout << "YES" << endl;
}
else
cout << "NO" << endl;
/* This Code is Contributed by Ankit Kumar*/
}
// Java program for the above approach
import java.io.*;
class GFG {
// Check if possible subset with
// given sum is possible or not
static int subsetSum(int a[], int n, int sum)
{
// Storing the value -1 to the matrix
int tab[][] = new int[n + 1][sum + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
tab[i][j] = -1;
}
}
// If the sum is zero it means
// we got our expected sum
if (sum == 0)
return 1;
if (n <= 0)
return 0;
// If the value is not -1 it means it
// already call the function
// with the same value.
// it will save our from the repetition.
if (tab[n - 1][sum] != -1)
return tab[n - 1][sum];
// If the value of a[n-1] is
// greater than the sum.
// we call for the next value
if (a[n - 1] > sum)
return tab[n - 1][sum]
= subsetSum(a, n - 1, sum);
else {
// Here we do two calls because we
// don't know which value is
// full-fill our criteria
// that's why we doing two calls
if (subsetSum(a, n - 1, sum) != 0
|| subsetSum(a, n - 1, sum - a[n - 1])
!= 0) {
return tab[n - 1][sum] = 1;
}
else
return tab[n - 1][sum] = 0;
}
}
// Driver Code
public static void main(String[] args)
{
int n = 5;
int a[] = { 1, 5, 3, 7, 4 };
int sum = 12;
if (subsetSum(a, n, sum) != 0) {
System.out.println("YES\n");
}
else
System.out.println("NO\n");
}
}
// This code is contributed by rajsanghavi9.
# Python program for the above approach
# Taking the matrix as globally
tab = [[-1 for i in range(2000)] for j in range(2000)]
# Check if possible subset with
# given sum is possible or not
def subsetSum(a, n, sum):
# If the sum is zero it means
# we got our expected sum
if (sum == 0):
return 1
if (n <= 0):
return 0
# If the value is not -1 it means it
# already call the function
# with the same value.
# it will save our from the repetition.
if (tab[n - 1][sum] != -1):
return tab[n - 1][sum]
# If the value of a[n-1] is
# greater than the sum.
# we call for the next value
if (a[n - 1] > sum):
tab[n - 1][sum] = subsetSum(a, n - 1, sum)
return tab[n - 1][sum]
else:
# Here we do two calls because we
# don't know which value is
# full-fill our criteria
# that's why we doing two calls
tab[n - 1][sum] = subsetSum(a, n - 1, sum)
return tab[n - 1][sum] or subsetSum(a, n - 1, sum - a[n - 1])
# Driver Code
if __name__ == '__main__':
n = 5
a = [1, 5, 3, 7, 4]
sum = 12
if (subsetSum(a, n, sum)):
print("YES")
else:
print("NO")
# This code is contributed by shivani.
// C# program for the above approach
using System;
class GFG
{
// Check if possible subset with
// given sum is possible or not
static int subsetSum(int []a, int n, int sum)
{
// Storing the value -1 to the matrix
int [,]tab = new int[n + 1,sum + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
tab[i,j] = -1;
}
}
// If the sum is zero it means
// we got our expected sum
if (sum == 0)
return 1;
if (n <= 0)
return 0;
// If the value is not -1 it means it
// already call the function
// with the same value.
// it will save our from the repetition.
if (tab[n - 1,sum] != -1)
return tab[n - 1,sum];
// If the value of a[n-1] is
// greater than the sum.
// we call for the next value
if (a[n - 1] > sum)
return tab[n - 1,sum]
= subsetSum(a, n - 1, sum);
else {
// Here we do two calls because we
// don't know which value is
// full-fill our criteria
// that's why we doing two calls
if (subsetSum(a, n - 1, sum) != 0
|| subsetSum(a, n - 1, sum - a[n - 1])
!= 0) {
return tab[n - 1,sum] = 1;
}
else
return tab[n - 1,sum] = 0;
}
}
// Driver Code
public static void Main(String[] args)
{
int n = 5;
int []a = { 1, 5, 3, 7, 4 };
int sum = 12;
if (subsetSum(a, n, sum) != 0) {
Console.Write("YES\n");
}
else
Console.Write("NO\n");
}
}
// This code is contributed by shivanisinghss2110
<script>
// JavaScript Program for the above approach
// Check if possible subset with
// given sum is possible or not
function subsetSum(a, n, sum) {
// If the sum is zero it means
// we got our expected sum
if (sum == 0)
return 1;
if (n <= 0)
return 0;
// If the value is not -1 it means it
// already call the function
// with the same value.
// it will save our from the repetition.
if (tab[n - 1][sum] != -1)
return tab[n - 1][sum];
// If the value of a[n-1] is
// greater than the sum.
// we call for the next value
if (a[n - 1] > sum)
return tab[n - 1][sum] = subsetSum(a, n - 1, sum);
else {
// Here we do two calls because we
// don't know which value is
// full-fill our criteria
// that's why we doing two calls
return tab[n - 1][sum] = subsetSum(a, n - 1, sum) ||
subsetSum(a, n - 1, sum - a[n - 1]);
}
}
// Driver Code
// Storing the value -1 to the matrix
let tab = Array(2000).fill().map(() => Array(2000).fill(-1));
let n = 5;
let a = [1, 5, 3, 7, 4];
let sum = 12;
if (subsetSum(a, n, sum)) {
document.write("YES" + "<br>");
}
else {
document.write("NO" + "<br>");
}
// This code is contributed by Potta Lokesh
</script>
Complexity Analysis:
- Time Complexity: O(sum*n), where sum is the ‘target sum’ and ‘n’ is the size of array.
- Auxiliary Space: O(sum*n) + O(n) -> O(sum*n) = the size of 2-D array is sum*n and O(n)=auxiliary stack space.
To solve the problem in Pseudo-polynomial time we can use the Dynamic programming approach.
So we will create a 2D array of size (n + 1) * (sum + 1) of type boolean. The state dp[i][j] will be true if there exists a subset of elements from set[0 . . . i] with sum value = ‘j’.
The dynamic programming relation is as follows:
if (A[i-1] > j)
dp[i][j] = dp[i-1][j]
else
dp[i][j] = dp[i-1][j] OR dp[i-1][j-set[i-1]]
This means that if the current element has a value greater than the ‘current sum value’ we will copy the answer for previous cases and if the current sum value is greater than the ‘ith’ element we will see if any of the previous states have already experienced the sum= j OR any previous states experienced a value ‘j – set[i]’ which will solve our purpose.
Illustration:
See the below illustration for a better understanding:
Consider set[] = {3, 4, 5, 2} and sum = 6.
The table will look like the following where the column number represents the sum and the row number represents the index of set[]:
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|---|
no element (0)
| T
| F
| F
| F
| F
| F
| F
|
|---|
|
0 (3)
| T
| F
| F
| T
| F
| F
| F
|
|---|
|
1 (4)
| T
| F
| F
| T
| T
| F
| F
|
|---|
|
2 (5)
| T
| F
| F
| T
| T
| T
| F
|
|---|
|
3 (2)
| T
| F
| T
| T
| T
| T
| T
|
|---|
Below is the implementation of the above approach:
C++
// A Dynamic Programming solution
// for subset sum problem
#include <bits/stdc++.h>
using namespace std;
// Returns true if there is a subset of set[]
// with sum equal to given sum
bool isSubsetSum(int set[], int n, int sum)
{
// The value of subset[i][j] will be true if
// there is a subset of set[0..j-1] with sum
// equal to i
bool subset[n + 1][sum + 1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[i][0] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
subset[0][i] = false;
// Fill the subset table in bottom up manner
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j < set[i - 1])
subset[i][j] = subset[i - 1][j];
if (j >= set[i - 1])
subset[i][j]
= subset[i - 1][j]
|| subset[i - 1][j - set[i - 1]];
}
}
return subset[n][sum];
}
// Driver code
int main()
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
cout << "Found a subset with given sum";
else
cout << "No subset with given sum";
return 0;
}
// This code is contributed by shivanisinghss2110
// A Dynamic Programming solution
// for subset sum problem
#include <stdio.h>
#include <stdbool.h>
// Returns true if there is a subset of set[]
// with sum equal to given sum
bool isSubsetSum(int set[], int n, int sum)
{
// The value of subset[i][j] will be true if
// there is a subset of set[0..j-1] with sum
// equal to i
bool subset[n + 1][sum + 1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[i][0] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
subset[0][i] = false;
// Fill the subset table in bottom up manner
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j < set[i - 1])
subset[i][j] = subset[i - 1][j];
if (j >= set[i - 1])
subset[i][j]
= subset[i - 1][j]
|| subset[i - 1][j - set[i - 1]];
}
}
return subset[n][sum];
}
// Driver code
int main()
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
printf("Found a subset with given sum");
else
printf("No subset with given sum");
return 0;
}
// This code is contributed by Arjun Tyagi.
// A Dynamic Programming solution for subset
// sum problem
import java.io.*;
class GFG {
// Returns true if there is a subset of
// set[] with sum equal to given sum
static boolean isSubsetSum(int set[], int n, int sum)
{
// The value of subset[i][j] will be
// true if there is a subset of
// set[0..j-1] with sum equal to i
boolean subset[][] = new boolean[sum + 1][n + 1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[0][i] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
subset[i][0] = false;
// Fill the subset table in bottom
// up manner
for (int i = 1; i <= sum; i++) {
for (int j = 1; j <= n; j++) {
subset[i][j] = subset[i][j - 1];
if (i >= set[j - 1])
subset[i][j]
= subset[i][j]
|| subset[i - set[j - 1]][j - 1];
}
}
return subset[sum][n];
}
// Driver code
public static void main(String args[])
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.length;
if (isSubsetSum(set, n, sum) == true)
System.out.println("Found a subset"
+ " with given sum");
else
System.out.println("No subset with"
+ " given sum");
}
}
/* This code is contributed by Rajat Mishra */
# A Dynamic Programming solution for subset
# sum problem Returns true if there is a subset of
# set[] with sun equal to given sum
# Returns true if there is a subset of set[]
# with sum equal to given sum
def isSubsetSum(set, n, sum):
# The value of subset[i][j] will be
# true if there is a
# subset of set[0..j-1] with sum equal to i
subset = ([[False for i in range(sum + 1)]
for i in range(n + 1)])
# If sum is 0, then answer is true
for i in range(n + 1):
subset[i][0] = True
# If sum is not 0 and set is empty,
# then answer is false
for i in range(1, sum + 1):
subset[0][i] = False
# Fill the subset table in bottom up manner
for i in range(1, n + 1):
for j in range(1, sum + 1):
if j < set[i-1]:
subset[i][j] = subset[i-1][j]
if j >= set[i-1]:
subset[i][j] = (subset[i-1][j] or
subset[i - 1][j-set[i-1]])
return subset[n][sum]
# Driver code
if __name__ == '__main__':
set = [3, 34, 4, 12, 5, 2]
sum = 9
n = len(set)
if (isSubsetSum(set, n, sum) == True):
print("Found a subset with given sum")
else:
print("No subset with given sum")
# This code is contributed by
# sahil shelangia.
// A Dynamic Programming solution for
// subset sum problem
using System;
class GFG {
// Returns true if there is a subset
// of set[] with sum equal to given sum
static bool isSubsetSum(int[] set, int n, int sum)
{
// The value of subset[i][j] will be true if there
// is a subset of set[0..j-1] with sum equal to i
bool[, ] subset = new bool[sum + 1, n + 1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[0, i] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
subset[i, 0] = false;
// Fill the subset table in bottom up manner
for (int i = 1; i <= sum; i++) {
for (int j = 1; j <= n; j++) {
subset[i, j] = subset[i, j - 1];
if (i >= set[j - 1])
subset[i, j]
= subset[i, j]
|| subset[i - set[j - 1], j - 1];
}
}
return subset[sum, n];
}
// Driver code
public static void Main()
{
int[] set = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.Length;
if (isSubsetSum(set, n, sum) == true)
Console.WriteLine(
"Found a subset with given sum");
else
Console.WriteLine("No subset with given sum");
}
}
// This code is contributed by Sam007
<script>
// A Dynamic Programming solution for subset sum problem
// Returns true if there is a subset of
// set[] with sum equal to given sum
function isSubsetSum(set, n, sum)
{
// The value of subset[i][j] will be
// true if there is a subset of
// set[0..j-1] with sum equal to i
let subset = new Array(sum + 1);
for(let i = 0; i < sum + 1; i++)
{
subset[i] = new Array(sum + 1);
for(let j = 0; j < n + 1; j++)
{
subset[i][j] = 0;
}
}
// If sum is 0, then answer is true
for (let i = 0; i <= n; i++)
subset[0][i] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (let i = 1; i <= sum; i++)
subset[i][0] = false;
// Fill the subset table in bottom
// up manner
for (let i = 1; i <= sum; i++) {
for (let j = 1; j <= n; j++) {
subset[i][j] = subset[i][j - 1];
if (i >= set[j - 1])
subset[i][j] = subset[i][j]
|| subset[i - set[j - 1]][j - 1];
}
}
return subset[sum][n];
}
let set = [ 3, 34, 4, 12, 5, 2 ];
let sum = 9;
let n = set.length;
if (isSubsetSum(set, n, sum) == true)
document.write("Found a subset" + " with given sum");
else
document.write("No subset with" + " given sum");
// This code is contributed by decode2207.
</script>
<?php
// A Dynamic Programming solution for
// subset sum problem
// Returns true if there is a subset of
// set[] with sum equal to given sum
function isSubsetSum( $set, $n, $sum)
{
// The value of subset[i][j] will
// be true if there is a subset of
// set[0..j-1] with sum equal to i
$subset = array(array());
// If sum is 0, then answer is true
for ( $i = 0; $i <= $n; $i++)
$subset[$i][0] = true;
// If sum is not 0 and set is empty,
// then answer is false
for ( $i = 1; $i <= $sum; $i++)
$subset[0][$i] = false;
// Fill the subset table in bottom
// up manner
for ($i = 1; $i <= $n; $i++)
{
for ($j = 1; $j <= $sum; $j++)
{
if($j < $set[$i-1])
$subset[$i][$j] =
$subset[$i-1][$j];
if ($j >= $set[$i-1])
$subset[$i][$j] =
$subset[$i-1][$j] ||
$subset[$i - 1][$j -
$set[$i-1]];
}
}
return $subset[$n][$sum];
}
// Driver code
$set = array(3, 34, 4, 12, 5, 2);
$sum = 9;
$n = count($set);
if (isSubsetSum($set, $n, $sum) == true)
echo "Found a subset with given sum";
else
echo "No subset with given sum";
// This code is contributed by anuj_67.
?>
OutputFound a subset with given sum
Complexity Analysis:
- Time Complexity: O(sum * n), where n is the size of the array.
- Auxiliary Space: O(sum*n), as the size of the 2-D array is sum*n.
Subset Sum Problem using Dynamic Programming with space optimization to linear:
Idea:
In previous approach of dynamic programming we have derive the relation between states as given below:
if (A[i-1] > j)
dp[i][j] = dp[i-1][j]
else
dp[i][j] = dp[i-1][j] OR dp[i-1][j-set[i-1]]
If we observe that for calculating current dp[i][j] state we only need previous row dp[i-1][j] or dp[i-1][j-set[i-1]].
There is no need to store all the previous states just one previous state is used to compute result.
Approach:
- Define two arrays prev and curr of size Sum+1 to store the just previous row result and current row result respectively.
- Once curr array is calculated then curr becomes our prev for the next row.
- When all rows are processed the answer is stored in prev array.
Implementation of the above approach:
C++
// A Dynamic Programming solution
// for subset sum problem with space optimization
#include <bits/stdc++.h>
using namespace std;
// Returns true if there is a subset of set[]
// with sum equal to given sum
bool isSubsetSum(int set[], int n, int sum)
{
vector<bool> prev(sum + 1);
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
prev[0] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
prev[i] = false;
// curr array to store the current row result generated
// with help of prev array
vector<bool> curr(sum + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j < set[i - 1])
curr[j] = prev[j];
if (j >= set[i - 1])
curr[j] = prev[j] || prev[j - set[i - 1]];
}
// now curr becomes prev for i+1 th element
prev = curr;
}
return prev[sum];
}
// Driver code
int main()
{
int set[] = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
cout << "Found a subset with given sum";
else
cout << "No subset with given sum";
return 0;
}
// This code is contributed by Hem Kishan
import java.util.Arrays;
public class SubsetSum {
// Returns true if there is a subset of set[]
// with a sum equal to the given sum
static boolean isSubsetSum(int[] set, int n, int sum) {
boolean[] prev = new boolean[sum + 1];
// If the sum is 0, the answer is true
for (int i = 0; i <= n; i++)
prev[0] = true;
// If the sum is not 0 and the set is empty,
// the answer is false
for (int i = 1; i <= sum; i++)
prev[i] = false;
// curr array to store the current row result generated
// with the help of the prev array
boolean[] curr = new boolean[sum + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j < set[i - 1])
curr[j] = prev[j];
if (j >= set[i - 1])
curr[j] = prev[j] || prev[j - set[i - 1]];
}
// now curr becomes prev for (i + 1)th element
prev = Arrays.copyOf(curr, curr.length);
}
return prev[sum];
}
// Driver code
public static void main(String[] args) {
int[] set = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.length;
if (isSubsetSum(set, n, sum))
System.out.println("Found a subset with the given sum");
else
System.out.println("No subset with the given sum");
}
}
// This code is contributed by shivamgupta0987654321
# Returns True if there is a subset of set[]
# with a sum equal to the given sum
def isSubsetSum(nums, n, sum):
# Create a list to store the previous row result
prev = [False] * (sum + 1)
# If sum is 0, then the answer is True
prev[0] = True
# If sum is not 0 and the set is empty,
# then the answer is False
for i in range(1, n + 1):
curr = [False] * (sum + 1)
for j in range(1, sum + 1):
if j < nums[i - 1]:
curr[j] = prev[j]
if j >= nums[i - 1]:
curr[j] = prev[j] or prev[j - nums[i - 1]]
# Now curr becomes prev for (i+1)-th element
prev = curr
return prev[sum]
# Driver code
if __name__ == "__main__":
nums = [3, 34, 4, 12, 5, 2]
sum_value = 9
n = len(nums)
if isSubsetSum(nums, n, sum_value):
print("Found a subset with the given sum")
else:
print("No subset with the given sum")
using System;
class Program
{
// Returns true if there is a subset of set[]
// with sum equal to given sum
static bool IsSubsetSum(int[] set, int n, int sum)
{
// Create a 2D array 'dp' with dimensions (n+1) x (sum+1)
bool[,] dp = new bool[n + 1, sum + 1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
dp[i, 0] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= sum; i++)
dp[0, i] = false;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= sum; j++)
{
if (j < set[i - 1])
dp[i, j] = dp[i - 1, j];
if (j >= set[i - 1])
dp[i, j] = dp[i - 1, j] || dp[i - 1, j - set[i - 1]];
}
}
return dp[n, sum];
}
static void Main()
{
int[] set = { 3, 34, 4, 12, 5, 2 };
int sum = 9;
int n = set.Length;
if (IsSubsetSum(set, n, sum))
Console.WriteLine("Found a subset with given sum");
else
Console.WriteLine("No subset with given sum");
}
}
// Returns true if there is a subset of set[]
// with sum equal to given sum
function isSubsetSum(set, n, sum) {
// Initialize a matrix to store subproblem results
let prev = new Array(sum + 1).fill(false);
// If sum is 0, then answer is true
prev[0] = true;
// curr array to store the current row result generated
// with help of prev array
let curr = [...prev];
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= sum; j++) {
if (j < set[i - 1]) {
curr[j] = prev[j];
}
if (j >= set[i - 1]) {
curr[j] = prev[j] || prev[j - set[i - 1]];
}
}
// now curr becomes prev for i+1 th element
prev = [...curr];
}
return prev[sum];
}
// Driver code
let set = [3, 34, 4, 12, 5, 2];
let sum = 9;
let n = set.length;
if (isSubsetSum(set, n, sum)) {
console.log("Found a subset with given sum");
} else {
console.log("No subset with given sum");
}
OutputFound a subset with given sum
Complexity Analysis:
- Time Complexity: O(sum * n), where n is the size of the array.
- Auxiliary Space: O(sum), as the size of the 1-D array is sum+1.
Related Articles:
Share your thoughts in the comments
Please Login to comment...