Why Prim’s and Kruskal’s MST algorithm fails for Directed Graph?
Last Updated :
31 Mar, 2020
Pre-requisites:
Given a directed graph D = < V, E >, the task is to find the minimum spanning tree for the given directed graph
Example:
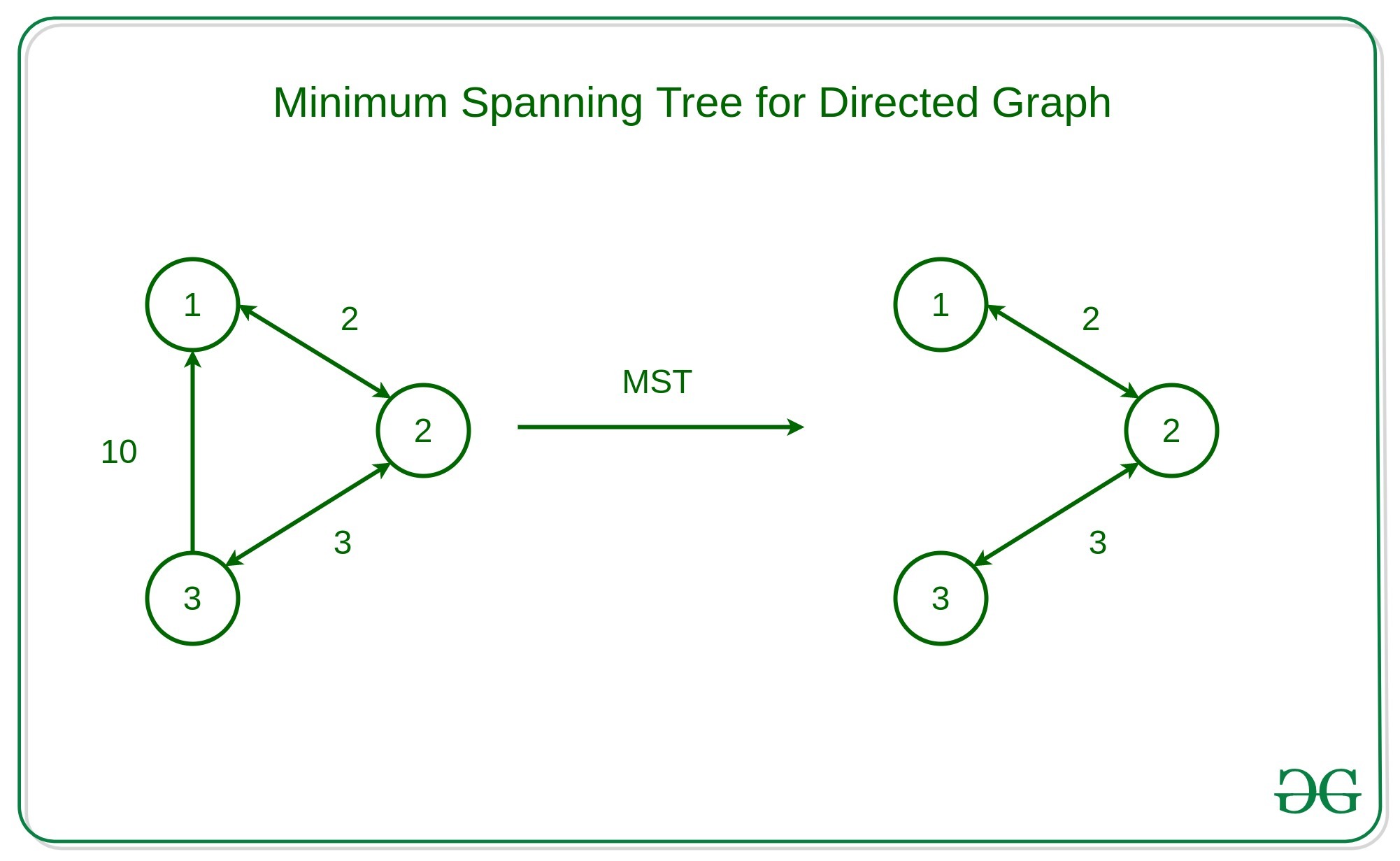
But the Prim’s Minimum Spanning Tree and Kruskal’s algorithm fails for directed graphs. Let us see why
Why Prim’s Algorithm Fails for Directed Graph ?
Prim’s algorithm assumes that all vertices are connected. But in a directed graph, every node is not reachable from every other node. So, Prim’s algorithm fails due to this reason.
For Example:
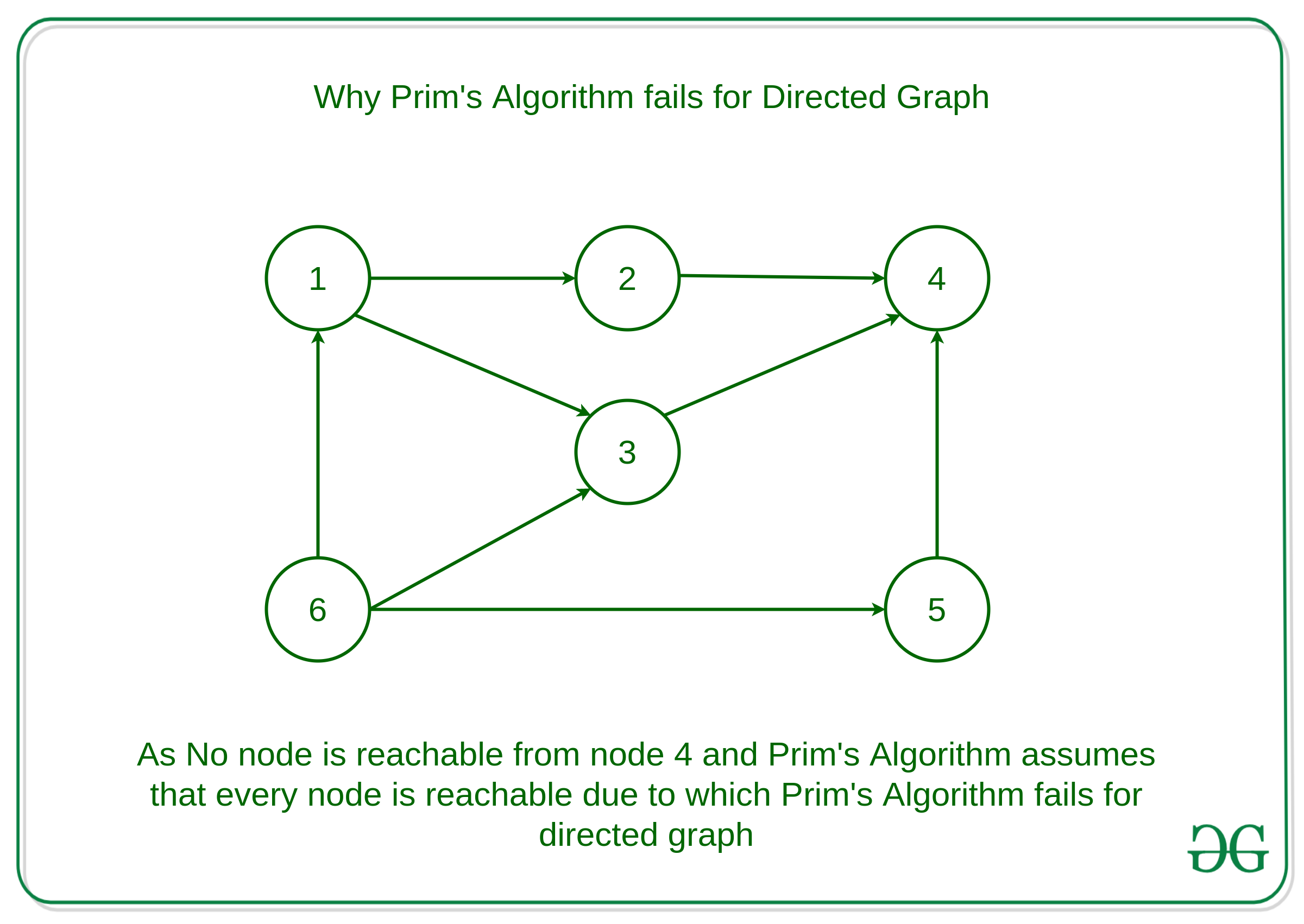
As it is visible in the graph, no node is reachable from node 4. Directed graphs fail the requirement that all vertices are connected.
Why Kruskal’s Algorithm fails for directed graph ?
In Kruskal’s algorithm, In each step, it is checked that if the edges form a cycle with the spanning-tree formed so far. But Kruskal’s algorithm fails to detect the cycles in a directed graph as there are cases when there is no cycle between the vertices but Kruskal’s Algorithm assumes it to cycle and don’t take consider some edges due to which Kruskal’s Algorithm fails for directed graph.
For example:
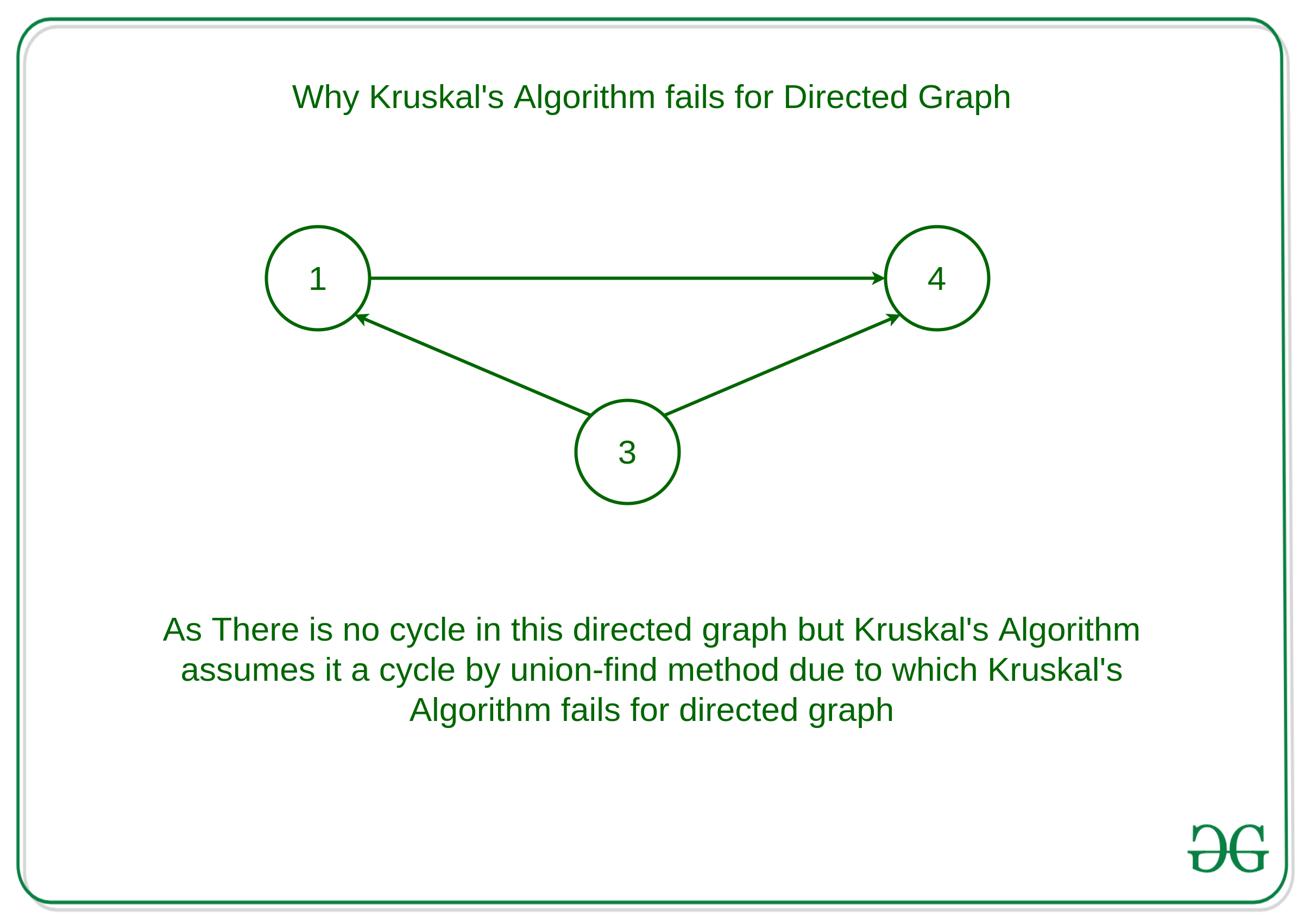
This graph will be reported to contain a cycle with the Union-Find method, but this graph has no cycle.
The equivalent of minimum spanning tree in directed graphs is, “Minimum Spanning Arborescence”(also known as optimum branching) can be solved by Edmonds’ algorithm with a running time of O(EV). This algorithm is directed analog of the minimum spanning tree problem.
Share your thoughts in the comments
Please Login to comment...