Ways to Remove Edges from a Complete Graph to make Odd Edges
Last Updated :
13 Mar, 2023
Given a complete graph with N vertices, the task is to count the number of ways to remove edges such that the resulting graph has odd number of edges.
Examples:
Input: N = 3
Output: 4
The initial graph has 3 edges as it is a complete graph. We can remove edges (1, 2) and (1, 3) or (1, 2) and (2, 3) or (1, 3) and (2, 3) or we do not remove any of the edges.
Input: N = 4
Output: 32
Approach: As the graph is complete so the total number of edges will be E = N * (N – 1) / 2. Now there are two cases,
- If E is even then you have to remove odd number of edges, so the total number of ways will be
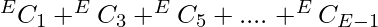 which is equivalent to
which is equivalent to 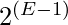 .
. - If E is odd then you have to remove even number of edges, so the total number of ways will be
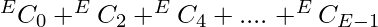 which is equivalent to
which is equivalent to 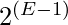 .
.
Note that if N = 1 then the answer will be 0.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countWays(int N)
{
int E = (N * (N - 1)) / 2;
if (N == 1)
return 0;
return pow(2, E - 1);
}
int main()
{
int N = 4;
cout << countWays(N);
return 0;
}
|
Java
class GfG
{
static int countWays(int N)
{
int E = (N * (N - 1)) / 2;
if (N == 1)
return 0;
return (int)Math.pow(2, E - 1);
}
public static void main(String[] args)
{
int N = 4;
System.out.println(countWays(N));
}
}
|
Python3
def countWays(N):
E = (N * (N - 1)) / 2
if (N == 1):
return 0
return int(pow(2, E - 1))
if __name__ == '__main__':
N = 4
print(countWays(N))
|
C#
using System;
public class GFG{
static int countWays(int N)
{
int E = (N * (N - 1)) / 2;
if (N == 1)
return 0;
return (int)Math.Pow(2, E - 1);
}
static public void Main (){
int N = 4;
Console.WriteLine(countWays(N));
}
}
|
PHP
<?php
function countWays($N)
{
$E = ($N * ($N - 1)) / 2;
if ($N == 1)
return 0;
return (int)pow(2, $E - 1);
}
$N = 4;
echo(countWays($N));
?>
|
Javascript
function countWays(N)
{
let E = (N * (N - 1)) / 2;
if (N == 1)
return 0;
return 2 ** (E - 1);
}
let N = 4;
console.log(countWays(N));
|
Time Complexity: O(log E), where E = (N * (N – 1)) / 2.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...