Ways of dividing a group into two halves such that two elements are in different groups
Last Updated :
25 Aug, 2022
Given 2n girls and randomly divided into two subgroups each containing n girls. The task is to count the number of ways in which groups can be formed such that two beautiful girls are into different groups.
Example:
Input: 4
Output: 4
Let group be r1, r2, b1, b2 where b1 and b2 are beautiful girls
Groups are: ((r1, b1) (r2, b2)), ((r1, b2) (r2, b1)), ((r2, b2) (r1, b1)), ((r2, b1) (r1, b2))
Input: 8
Output: 40
Approach: There are two ways in which the two beautiful girls lie in different groups and corresponding to each way the remaining (2n – 2) girls can be divided into two groups is 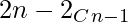
Hence total number of ways are 2 * 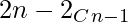
Implementation Code :
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
int result = 1;
for (int i = 1; i <= n; i++)
result = result * i;
return result;
}
int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
int calculate_result(int n)
{
int result = 2 * nCr((n - 2), (n / 2 - 1));
return result;
}
int main(void)
{
int a = 2, b = 4;
cout << calculate_result(2 * a) << endl;
cout << calculate_result(2 * b) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static int factorial(int n)
{
int result = 1;
for (int i = 1; i <= n; i++)
result = result * i;
return result;
}
static int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
static int calculate_result(int n)
{
int result = 2 * nCr((n - 2), (n / 2 - 1));
return result;
}
public static void main (String[] args) {
int a = 2, b = 4;
System.out.println( calculate_result(2 * a));
System.out.print(calculate_result(2 * b));
}
}
|
Python3
def factorial(n) :
result = 1
for i in range(1, n + 1) :
result *= i
return result
def nCr(n, r) :
return (factorial(n) // (factorial(r)
* factorial(n - r)))
def calculate_result(n) :
result = 2 * nCr((n -2), (n // 2 - 1))
return result
if __name__ == "__main__" :
a, b = 2, 4
print(calculate_result(2 * a))
print(calculate_result(2 * b))
|
C#
using System;
public class GFG {
static int factorial(int n)
{
int result = 1;
for (int i = 1; i <= n; i++)
result = result * i;
return result;
}
static int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
static int calculate_result(int n)
{
int result = 2 * nCr((n - 2), (n / 2 - 1));
return result;
}
public static void Main () {
int a = 2, b = 4;
Console.WriteLine( calculate_result(2 * a));
Console.Write(calculate_result(2 * b));
}
}
|
PHP
<?php
function factorial($n)
{
$result = 1;
for ($i = 1; $i <= $n; $i++)
$result = $result * $i;
return $result;
}
function nCr($n, $r)
{
return factorial($n) / (factorial($r) *
factorial($n - $r));
}
function calculate_result($n)
{
$result = 2 * nCr(($n - 2),
($n / 2 - 1));
return $result;
}
$a = 2;
$b = 4;
echo calculate_result(2 * $a) . "\n";
echo calculate_result(2 * $b) . "\n";
?>
|
Javascript
function factorial(n)
{
let result = 1;
for (let i = 1; i <= n; i++)
result = result * i;
return result;
}
function nCr(n, r)
{
return factorial(n) / (factorial(r) *
factorial(n - r));
}
function calculate_result(n)
{
let result = 2 * nCr((n - 2),
(n / 2 - 1));
return result;
}
let a = 2;
let b = 4;
document.write(calculate_result(2 * a) + "<br>");
document.write(calculate_result(2 * b) + "<br>");
|
Time Complexity: O(N), since the loop runs for N times.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...