Volume of cube using its space diagonal
Last Updated :
24 Jun, 2022
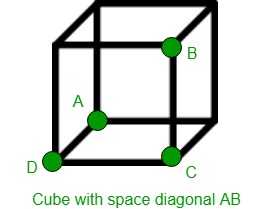
Given the length of space diagonal of a cube as d. The task is to calculate the volume occupied by the cube with the given length of space diagonal. Space diagonal is a line connecting two vertices that are not on the same face.
Examples:
Input: d = 5
Output: Volume of Cube: 24.0563
Input: d = 10
Output: Volume of Cube: 192.45
Volume of cube whose space diagonal is given: 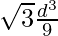
Proof:
Let d = the length of diagonal |AB| and
let a = the length of each side of the cube.
Pythagoras #1 in triangle ACD:
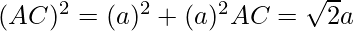
Pythagoras #2 in triangle ABC:
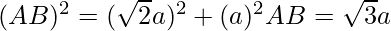
Now we can solve for a in terms of d:
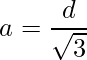
This means that the volume V is:
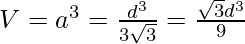
Below is the required implementation:
C++
#include <bits/stdc++.h>
using namespace std;
float CubeVolume(float d)
{
float Volume;
Volume = (sqrt(3) * pow(d, 3)) / 9;
return Volume;
}
int main()
{
float d = 5;
cout << "Volume of Cube: "
<< CubeVolume(d);
return 0;
}
|
Java
public class GFG{
static float CubeVolume(float d)
{
float Volume;
Volume = (float) (Math.sqrt(3) * Math.pow(d, 3)) / 9;
return Volume;
}
public static void main(String []args)
{
float d = 5;
System.out.println("Volume of Cube: " + CubeVolume(d));
}
}
|
Python3
from math import sqrt, pow
def CubeVolume(d):
Volume = (sqrt(3) * pow(d, 3)) / 9
return Volume
if __name__ == '__main__':
d = 5
print("Volume of Cube:",'{0:.6}' .
format(CubeVolume(d)))
|
C#
using System;
public class GFG{
static float CubeVolume(float d)
{
float Volume;
Volume = (float) (Math.Sqrt(3) * Math.Pow(d, 3)) / 9;
return Volume;
}
public static void Main()
{
float d = 5;
Console.WriteLine("Volume of Cube: {0:F4}" , CubeVolume(d));
}
}
|
PHP
<?php
function CubeVolume($d)
{
$Volume;
$Volume = (sqrt(3) * pow($d, 3)) / 9;
return $Volume;
}
$d = 5;
echo "Volume of Cube: ",
CubeVolume($d);
?>
|
Javascript
<script>
function CubeVolume( d)
{
let Volume;
Volume = (Math.sqrt(3) * Math.pow(d, 3)) / 9;
return Volume;
}
let d = 5;
document.write( "Volume of Cube: "
+ CubeVolume(d).toFixed(4));
</script>
|
Output: Volume of Cube: 24.0563
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...