Vector Projection using Python
Last Updated :
29 Nov, 2019
A vector is a geometric object which has both magnitude (i.e. length) and direction. A vector is generally represented by a line segment with a certain direction connecting the initial point A and the terminal point B as shown in the figure below and is denoted by
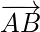

Projection of a Vector on another vector
The projection of a vector
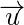
onto another vector
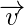
is given as
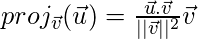 Computing vector projection onto another vector in Python:
Computing vector projection onto another vector in Python:
import numpy as np
u = np.array([1, 2, 3])
v = np.array([5, 6, 2])
v_norm = np.sqrt(sum(v**2))
proj_of_u_on_v = (np.dot(u, v)/v_norm**2)*v
print("Projection of Vector u on Vector v is: ", proj_of_u_on_v)
|
Output:
Projection of Vector u on Vector v is: [1.76923077 2.12307692 0.70769231]
One liner code for projecting a vector onto another vector:
(np.dot(u, v)/np.dot(v, v))*v
|
Projection of a Vector onto a Plane
The projection of a vector
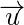
onto a plane is calculated by subtracting the component of
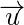
which is orthogonal to the plane from
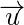
.
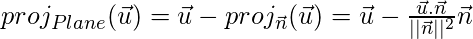
where,
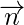
is the plane normal vector.
Computing vector projection onto a Plane in Python:
import numpy as np
u = np.array([2, 5, 8])
n = np.array([1, 1, 7])
n_norm = np.sqrt(sum(n**2))
proj_of_u_on_n = (np.dot(u, n)/n_norm**2)*n
print("Projection of Vector u on Plane P is: ", u - proj_of_u_on_n)
|
Output:
Projection of Vector u on Plane P is: [ 0.76470588 3.76470588 -0.64705882]
Share your thoughts in the comments
Please Login to comment...