Understanding Murphy’s law with proofs and examples
Last Updated :
13 Apr, 2021
In this article, we will discuss the overview of layman’s terms, Murphy’s law, and then we will mainly focus on proof and explanations and will understand Murphy’s law with proofs and example. Let’s discuss it one by one.
Overview :
In layman’s terms, Murphy’s law says that “If something can go wrong, it will go wrong “. Mathematically, Given mutually independent events A1, A2, …. An.
And T = number of events to occur,
Ex( T ) denotes the expected number of events to occur.
Then Murphy’s law says that Probability that none of the independent events will occur is upper bounded by this expression as follows.
e^( -Ex(T)).
or
P( T =0 ) ≤ e ∧-Ex(T)
Proof :
In the proof, Ai represents i= 1,2…n everywhere.
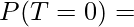 [Tex]P(A1' ∩ A2' ∩ ......An')[/Tex]
[Tex]P(A1' ∩ A2' ∩ ......An')[/Tex]
= ∏ (P(Ai') ) for i= 1,2....n
= ∏ (1-P(Ai)) step 3
≤ ∏ (e^-P(Ai)) step 4
≤ e ^[∑ (-P(Ai))] step 5
≤ e ^ -Ex(T) step 6Proof Explanation :
To understand step 3 to 4, read a bit about Taylor’s series, Using Taylor’s series for e^-x and using Approximation as follows.
e^-x ≥ 1-x
= 1-x ≤ e^-x , In our case, x is equivalent to P(Ai)
To understand step 4 to 5 –
∏ (e^-P(Ai))
= e^-P(A1) * e^-P(A2) * e^-P(A3) ....... e^-P(An)
= e^-{A1+A2+A3 +.....+An}
= e ^[∑ (-P(Ai))]To understand step 5 to 6 –
Recall the definition of the Number of Expected number of events to occur as follows.
= Ex(T) = ∑ (P(Ai)) for i= 1 to n.
Hence, proved. Given a probability space S and events A1, A2 …. An. Are in S. Then following expression as follows.
Expected number of events to occur = Ex(T) = ∑ P(Ai) for i = 1...n
Now that we have proved Murphy’s law.
Example-1 :
Let’s look at one example to understand this. Let us say that there are one thousand events responsible for the failure of a nuclear reactor, the expected value of the number of events to occur is 10. Assuming all the events are mutually independent. Then what is the probability that none of these factors will happen and thus no failure?
Solution –
From the question, we know that Ex(T) =10 where T = Expected number of events to cause failure. The probability that none of the events will happen according to Murphy’s law is upper bounded by e-10 which is 0.000045. So, chances that at least one event will cause failure is = 1- e-10 = 0.999955. This is the impact of Murphy’s law, and it’s a very important concept in mathematics for computer science students.
References :
https://en.wikipedia.org/wiki/Taylor_series
Share your thoughts in the comments
Please Login to comment...