Understanding Chebyshev’s inequality with an example
Last Updated :
08 Apr, 2021
In this article, we will discuss the overview of Chebyshev’s inequality algorithm, and will cover the Understanding Chebyshev’s inequality with an example. Pre-requisite is to go to given below link to understand Markov’s theorem to get more deep mathematical insights behind the Chebyshev’s inequality, and it’s proof. Let’s discuss it one by one.
Pre-requisite – Understanding Markov’s theorem with example
Chebyshev’s inequality :
It is based on the concept of variance. It says that given a random variable R, then ∀ x > 0, The probability that the random variable R deviates from its expected value in either side by at least x is given as follows.
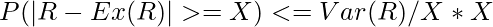 //equation -1
//equation -1
Where it represents the following values as follows.
Var(R) - It denotes variance of Random Variable R.
Ex(R) - It denotes the Expected value of Random Variable R.
Proof :
We know Markov’s inequality in Probability as follows.
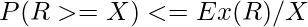 //equation -2
//equation -2
Put : R – Ex(R) in place of R in this and square this and then apply Markov’s inequality, we get the following expression as follows.
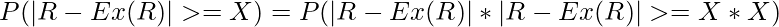 //equation -3
//equation -3
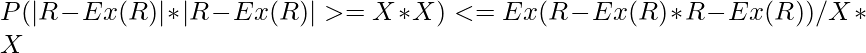 //equation -4
//equation -4
We also know that the following expression and with the help of this we can evaluate.
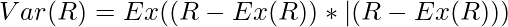
Now, put this in the fourth equation and replace LHS of the fourth equation with LHS of the third equation, we get Chebychev’s inequality as follows.
Result :
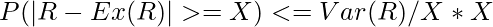
Corollary of Chebyshev’s inequality :
If we replace X with c*Var(R), where c > 0 ,then we get the below equation which can be proven very easily as follows.
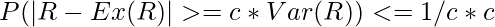
Example of Chebyshev’s inequality :
Let’s understand the concept with the help of an example for better understanding as follows.
Example-1 :
Let us say that Random Variable R = IQ of a random person. And average IQ of a person is 100, i.e, Ex(R) = 100. And Variance in R is 15. (Assuming R >0). Then what is the probability that if we pick a random person, his/her IQ is at least 250 ?
Solution –
To solve this, we will use corollary of the Chebyshev’s inequality as follows.
P(R>=250) = P( R-100 >=150 ),
Comparing with the Corollary, we can say that the following result as follows.
since 150 = 10* Variance
so, c = 10.
Therefore, answer is upper bounded by 1/100 which is ≤1 %.
Example-2 :
If we solve the same problem using Markov’s theorem without using the variance, we get the upper bound as follows.
P ( R >= 250 ) < = Ex(R) / 250
= 100/250 = 2/5 = 40%.
So, the Same problem is upper bounded by 40 % by Markov’s inequality and by 1% by Chebyshev’s inequality. Thus, we can say that Chebyshev’s inequality gives a better bound on probability compared to Markov’s if we know the variance of random variable R.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...