Threaded Binary Tree
Last Updated :
26 Mar, 2024
Inorder traversal of a Binary tree can either be done using recursion or with the use of a auxiliary stack. The idea of threaded binary trees is to make inorder traversal faster and do it without stack and without recursion. A binary tree is made threaded by making all right child pointers that would normally be NULL point to the inorder successor of the node (if it exists).
A threaded binary tree is a type of binary tree data structure where the empty left and right child pointers in a binary tree are replaced with threads that link nodes directly to their in-order predecessor or successor, thereby providing a way to traverse the tree without using recursion or a stack.
Threaded binary trees can be useful when space is a concern, as they can eliminate the need for a stack during traversal. However, they can be more complex to implement than standard binary trees.
There are two types of threaded binary trees.
Single Threaded: Where a NULL right pointers is made to point to the inorder successor (if successor exists)
Double Threaded: Where both left and right NULL pointers are made to point to inorder predecessor and inorder successor respectively. The predecessor threads are useful for reverse inorder traversal and postorder traversal.
The threads are also useful for fast accessing ancestors of a node.
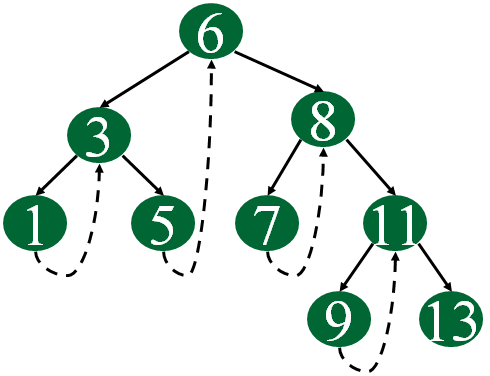
Following diagram shows an example Single Threaded Binary Tree. The dotted lines represent threads.
C and C++ representation of a Threaded Node
Following is C and C++representation of a single-threaded node.
C++
// Use any below method to represent a Threaded Node
// Method 1: Using "struct" to make
// user-define data type
struct node {
int data;
struct node* left;
struct node* right;
bool rightThread;
};
// Method 2: Using "class" to make
// user-define data type
class Node {
public:
int data;
Node* left;
Node* right;
bool rightThread;
// Val is the key or the value that has to be added to
// the data part
Node(int val){
data = val;
// Left and right child for node will be initialized
// to null
left = NULL;
right = NULL;
// rightThread will be initialized to false
rightThread = false;
}
};
// This code is contributed by Susobhan Akhuli
typedef struct Node {
int data;
struct Node* left;
struct Node* right;
bool rightThread;
} Node;
// Constructor function
Node* createNode(int val) {
Node* newNode = (Node*)malloc(sizeof(Node));
if (newNode != NULL) {
newNode->data = val;
newNode->left = NULL;
newNode->right = NULL;
newNode->rightThread = false;
}
return newNode;
}
// Method 1: Using "struct" to define a threaded node
class ThreadedNode1 {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
this.rightThread = false;
}
}
// Method 2: Using "class" to define a threaded node
class ThreadedNode2 {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
this.rightThread = false;
}
}
Java representation of a Threaded Node
Following is Java representation of a single-threaded node.
Java
static class Node
{
int data;
Node left, right;
boolean rightThread;
}
// This code contributed by aashish1995
Python3 representation of a Threaded Node
Following is Python3 representation of a single-threaded node.
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
self.rightThread = False
Since right pointer is used for two purposes, the boolean variable rightThread is used to indicate whether right pointer points to right child or inorder successor. Similarly, we can add leftThread for a double threaded binary tree.
Inorder Traversal using Threads
Following is code for inorder traversal in a threaded binary tree.
C++
// Utility function to find leftmost node in a tree rooted with n
Node* leftMost(Node* n){
if (n == NULL)
return NULL;
while (n->left != NULL)
n = n->left;
return n;
}
// CPP code to do inorder traversal in a threaded binary tree
void inOrder(Node* root){
Node* cur = leftMost(root);
while (cur != NULL) {
cout<<cur->data<<" ";
// If this node is a thread node, then go to
// inorder successor
if (cur->rightThread)
cur = cur->right;
else // Else go to the leftmost child in right
// subtree
cur = leftmost(cur->right);
}
}
// This code is contributed by Susobhan Akhuli
// Utility function to find leftmost node in a tree rooted
// with n
struct Node* leftMost(struct Node* n)
{
if (n == NULL)
return NULL;
while (n->left != NULL)
n = n->left;
return n;
}
// C code to do inorder traversal in a threaded binary tree
void inOrder(struct Node* root)
{
struct Node* cur = leftMost(root);
while (cur != NULL) {
printf("%d ", cur->data);
// If this node is a thread node, then go to
// inorder successor
if (cur->rightThread)
cur = cur->right;
else // Else go to the leftmost child in right
// subtree
cur = leftmost(cur->right);
}
}
// Utility function to find leftmost node in a tree rooted
// with n
Node leftMost(Node n)
{
if (n == null)
return null;
while (n.left != null)
n = n.left;
return n;
}
// C code to do inorder traversal in a threaded binary tree
static void inOrder(Node root)
{
Node cur = leftMost(root);
while (cur != null) {
System.out.printf("%d ", cur.data);
// If this node is a thread node, then go to
// inorder successor
if (cur.rightThread)
cur = cur.right;
else // Else go to the leftmost child in right
// subtree
cur = leftmost(cur.right);
}
}
// This code contributed by aashish1995
// Utility function to find leftmost node in a tree rooted
// with n
Node leftMost(Node n)
{
if (n == null)
return null;
while (n.left != null)
n = n.left;
return n;
}
// C code to do inorder traversal in a threaded binary tree
static void inOrder(Node root)
{
Node cur = leftMost(root);
while (cur != null)
{
Console.Write("{0} ", cur.data);
// If this node is a thread node, then go to
// inorder successor
if (cur.rightThread)
cur = cur.right;
else // Else go to the leftmost child in right
// subtree
cur = leftmost(cur.right);
}
}
// This code is contributed by gauravrajput1
<script>
// Utility function to find leftmost node in a tree rooted
// with n
function leftMost(n)
{
if (n == null)
return null;
while (n.left != null)
n = n.left;
return n;
}
// JavaScript code to do inorder traversal in
// a threaded binary tree
function inOrder(root)
{
let cur = leftMost(root);
while (cur != null) {
document.write(cur.data+" ");
// If this node is a thread node, then go to
// inorder successor
if (cur.rightThread)
cur = cur.right;
else // Else go to the leftmost child in right
// subtree
cur = leftmost(cur.right);
}
}
// This code is contributed by unknown2108
</script>
# Utility function to find leftmost Node in a tree rooted
# with n
def leftMost(n):
if (n == None):
return None;
while (n.left != None):
n = n.left;
return n;
# C code to do inorder traversal in a threaded binary tree
def inOrder(root):
cur = leftMost(root);
while (cur != None):
print(cur.data," ");
# If this Node is a thread Node, then go to
# inorder successor
if (cur.rightThread):
cur = cur.right;
else: # Else go to the leftmost child in right
# subtree
cur = leftmost(cur.right);
# This code is contributed by Rajput-Ji
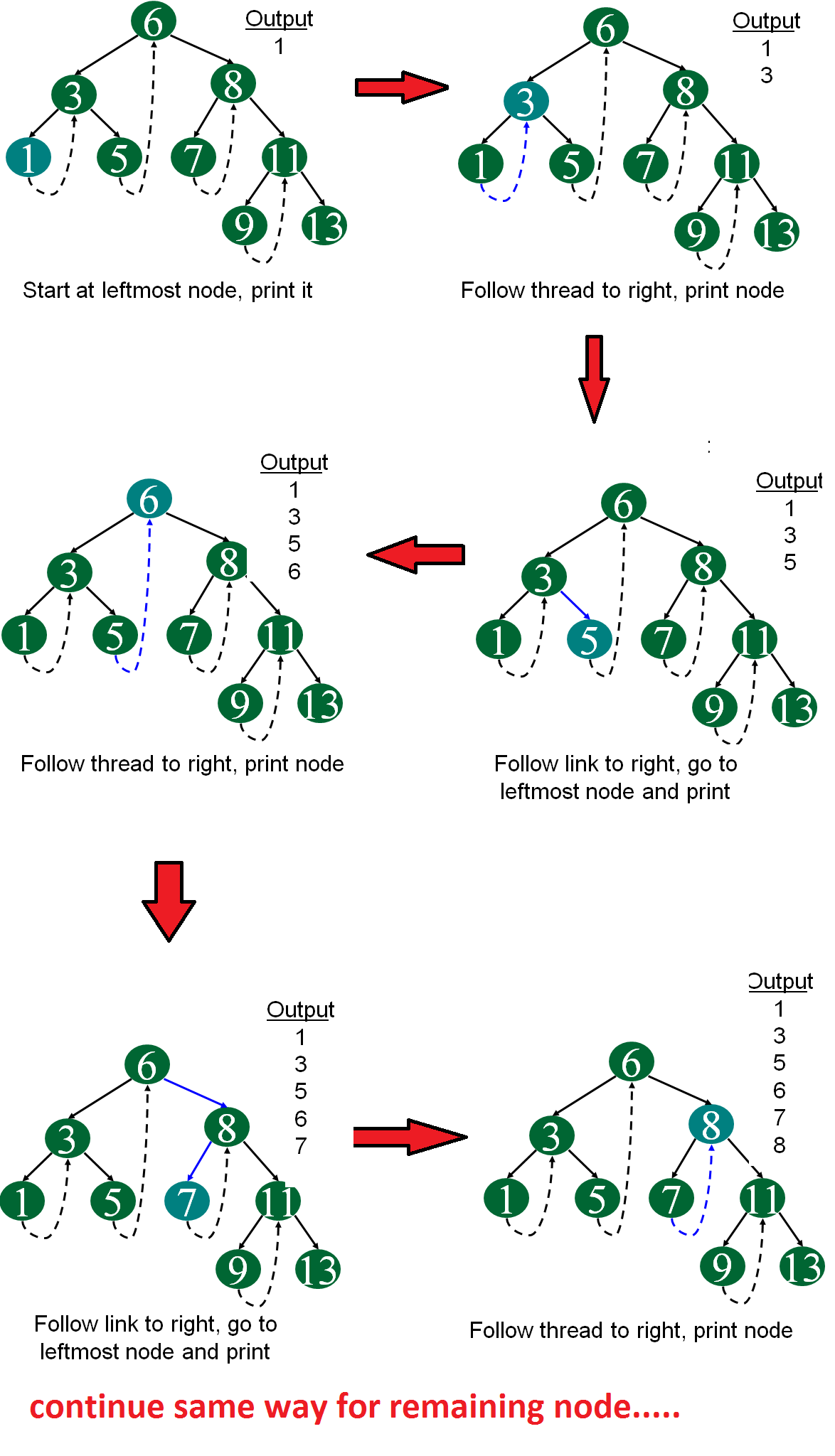
Following diagram demonstrates inorder order traversal using threads.
Advantages of Threaded Binary Tree
- In this Tree it enables linear traversal of elements.
- It eliminates the use of stack as it perform linear traversal, so save memory.
- Enables to find parent node without explicit use of parent pointer
- Threaded tree give forward and backward traversal of nodes by in-order fashion
- Nodes contain pointers to in-order predecessor and successor
- For a given node, we can easily find inorder predecessor and successor. So, searching is much more easier.
- In threaded binary tree there is no NULL pointer present. Hence memory wastage in occupying NULL links is avoided.
- The threads are pointing to successor and predecessor nodes. This makes us to obtain predecessor and successor node of any node quickly.
- There is no need of stack while traversing the tree, because using thread links we can reach to previously visited nodes.
Disadvantages of Threaded Binary Tree
- Every node in threaded binary tree need extra information(extra memory) to indicate whether its left or right node indicated its child nodes or its inorder predecessor or successor. So, the node consumes extra memory to implement.
- Insertion and deletion are way more complex and time consuming than the normal one since both threads and ordinary links need to be maintained.
- Implementing threads for every possible node is complicated.
- Increased complexity: Implementing a threaded binary tree requires more complex algorithms and data structures than a regular binary tree. This can make the code harder to read and debug.
- Extra memory usage: In some cases, the additional pointers used to thread the tree can use up more memory than a regular binary tree. This is especially true if the tree is not fully balanced, as threading a skewed tree can result in a large number of additional pointers.
- Limited flexibility: Threaded binary trees are specialized data structures that are optimized for specific types of traversal. While they can be more efficient than regular binary trees for these types of operations, they may not be as useful in other scenarios. For example, they cannot be easily modified (e.g. inserting or deleting nodes) without breaking the threading.
- Difficulty in parallelizing: It can be challenging to parallelize operations on a threaded binary tree, as the threading can introduce data dependencies that make it difficult to process nodes independently. This can limit the performance gains that can be achieved through parallelism.
Applications of threaded binary tree –
- Expression evaluation: Threaded binary trees can be used to evaluate arithmetic expressions in a way that avoids recursion or a stack. The tree can be constructed from the input expression, and then traversed in-order or pre-order to perform the evaluation.
- Database indexing: In a database, threaded binary trees can be used to index data based on a specific field (e.g. last name). The tree can be constructed with the indexed values as keys, and then traversed in-order to retrieve the data in sorted order.
- Symbol table management: In a compiler or interpreter, threaded binary trees can be used to store and manage symbol tables for variables and functions. The tree can be constructed with the symbols as keys, and then traversed in-order or pre-order to perform various operations on the symbol table.
- Disk-based data structures: Threaded binary trees can be used in disk-based data structures (e.g. B-trees) to improve performance. By threading the tree, it can be traversed in a way that minimizes disk seeks and improves locality of reference.
- Navigation of hierarchical data: In certain applications, threaded binary trees can be used to navigate hierarchical data structures, such as file systems or web site directories. The tree can be constructed from the hierarchical data, and then traversed in-order or pre-order to efficiently access the data in a specific order.
We will soon be discussing insertion and deletion in threaded binary trees.
Sources:
http://en.wikipedia.org/wiki/Threaded_binary_tree
www.cs.berkeley.edu/~kamil/teaching/su02/080802.ppt
Share your thoughts in the comments
Please Login to comment...