Convert a Binary Tree to Threaded binary tree | Set 2 (Efficient)

Difficulty Level : Medium
Last Updated : 24 Nov, 2021

Idea of Threaded Binary Tree is to make inorder traversal faster and do it without stack and without recursion. In a simple threaded binary tree, the NULL right pointers are used to store inorder successor. Where-ever a right pointer is NULL, it is used to store inorder successor.
Following diagram shows an example Single Threaded Binary Tree. The dotted lines represent threads.

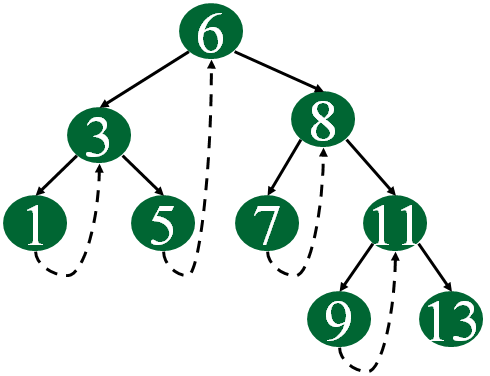
threadedBT

Following is structure of a single-threaded binary tree.

C

struct Node
{
    int key;
    Node *left, *right;
 
    // Used to indicate whether the right pointer is a normal right
    // pointer or a pointer to inorder successor.
    bool isThreaded;
};

Java

static class Node
{
    int key;
    Node left, right;
 
    // Used to indicate whether the right pointer is a normal right
    // pointer or a pointer to inorder successor.
    boolean isThreaded;
};
 
// This code is contributed by umadevi9616

Python3

class Node:
    def __init__(self, data):
        self.key = data;
        self.left = none;
        self.right = none;
        self.isThreaded = false;
    # Used to indicate whether the right pointer is a normal right
    # pointer or a pointer to inorder successor.
 
# This code is contributed by umadevi9616

C#

public class Node {
    public int key;
    public Node left, right;
 
    // Used to indicate whether the right pointer is a normal right
    // pointer or a pointer to inorder successor.
    public bool isThreaded;
};
 
 
// This code is contributed by umadevi9616

Javascript

/* structure of a node in threaded binary tree */
 class Node {
        constructor(val) {
            this.data = val;
            this.left = null;
            this.right = null;
     
   
    // Used to indicate whether the right pointer
    // is a normal right pointer or a pointer
    // to inorder successor.
    this.isThreaded = false;
    }
    }
     
    // This code is contributed by famously.

How to convert a Given Binary Tree to Threaded Binary Tree?
We have discussed a Queue-based solution here. In this post, space-efficient solution is discussed that doesn’t require a queue.
The idea is based on the fact that we link from inorder predecessor to a node. We link those inorder predecessor which lie in subtree of node. So we find inorder predecessor of a node if its left is not NULL. Inorder predecessor of a node (whose left is NULL) is a rightmost node in the left child. Once we find the predecessor, we link a thread from it to the current node.
Following is the implementation of the above idea.

C++

/* C++ program to convert a Binary Tree to
    Threaded Tree */
#include <bits/stdc++.h>
using namespace std;
 
/* Structure of a node in threaded binary tree */
struct Node
{
    int key;
    Node *left, *right;
 
    // Used to indicate whether the right pointer
    // is a normal right pointer or a pointer
    // to inorder successor.
    bool isThreaded;
};
 
// Converts tree with given root to threaded
// binary tree.
// This function returns rightmost child of
// root.
Node *createThreaded(Node *root)
{
    // Base cases : Tree is empty or has single
    //              node
    if (root == NULL)
        return NULL;
    if (root->left == NULL &&
        root->right == NULL)
        return root;
 
    // Find predecessor if it exists
    if (root->left != NULL)
    {
        // Find predecessor of root (Rightmost
        // child in left subtree)
        Node* l = createThreaded(root->left);
 
        // Link a thread from predecessor to
        // root.
        l->right = root;
        l->isThreaded = true;
    }
 
    // If current node is rightmost child
    if (root->right == NULL)
        return root;
 
    // Recur for right subtree.
    return createThreaded(root->right);
}
 
// A utility function to find leftmost node
// in a binary tree rooted with 'root'.
// This function is used in inOrder()
Node *leftMost(Node *root)
{
    while (root != NULL && root->left != NULL)
        root = root->left;
    return root;
}
 
// Function to do inorder traversal of a threadded
// binary tree
void inOrder(Node *root)
{
    if (root == NULL) return;
 
    // Find the leftmost node in Binary Tree
    Node *cur = leftMost(root);
 
    while (cur != NULL)
    {
        cout << cur->key << " ";
 
        // If this Node is a thread Node, then go to
        // inorder successor
        if (cur->isThreaded)
            cur = cur->right;
 
        else // Else go to the leftmost child in right subtree
            cur = leftMost(cur->right);
    }
}
 
// A utility function to create a new node
Node *newNode(int key)
{
    Node *temp = new Node;
    temp->left = temp->right = NULL;
    temp->key = key;
    return temp;
}
 
// Driver program to test above functions
int main()
{
    /*       1
            / \
           2   3
          / \ / \
         4  5 6  7   */
    Node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
 
    createThreaded(root);
 
    cout << "Inorder traversal of created "
            "threaded tree is\n";
    inOrder(root);
    return 0;
}

Java

/* Java program to convert a Binary Tree to
    Threaded Tree */
import java.util.*;
class solution
{
  
   
/* structure of a node in threaded binary tree */
static class Node
{
    int key;
    Node left, right;
   
    // Used to indicate whether the right pointer
    // is a normal right pointer or a pointer
    // to inorder successor.
    boolean isThreaded;
};
   
// Converts tree with given root to threaded
// binary tree.
// This function returns rightmost child of
// root.
static Node createThreaded(Node root)
{
    // Base cases : Tree is empty or has single
    //              node
    if (root == null)
        return null;
    if (root.left == null &&
        root.right == null)
        return root;
   
    // Find predecessor if it exists
    if (root.left != null)
    {
        // Find predecessor of root (Rightmost
        // child in left subtree)
        Node l = createThreaded(root.left);
   
        // Link a thread from predecessor to
        // root.
        l.right = root;
        l.isThreaded = true;
    }
   
    // If current node is rightmost child
    if (root.right == null)
        return root;
   
    // Recur for right subtree.
    return createThreaded(root.right);
}
   
// A utility function to find leftmost node
// in a binary tree rooted with 'root'.
// This function is used in inOrder()
static Node leftMost(Node root)
{
    while (root != null && root.left != null)
        root = root.left;
    return root;
}
   
// Function to do inorder traversal of a threadded
// binary tree
static void inOrder(Node root)
{
    if (root == null) return;
   
    // Find the leftmost node in Binary Tree
    Node cur = leftMost(root);
   
    while (cur != null)
    {
        System.out.print(cur.key + " ");
   
        // If this Node is a thread Node, then go to
        // inorder successor
        if (cur.isThreaded)
            cur = cur.right;
   
        else // Else go to the leftmost child in right subtree
            cur = leftMost(cur.right);
    }
}
   
// A utility function to create a new node
static Node newNode(int key)
{
    Node temp = new Node();
    temp.left = temp.right = null;
    temp.key = key;
    return temp;
}
   
// Driver program to test above functions
public static void main(String args[])
{
   /*       1
            / \
           2   3
          / \ / \
         4  5 6  7   */
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
    root.right.left = newNode(6);
    root.right.right = newNode(7);
   
    createThreaded(root);
   
    System.out.println("Inorder traversal of created "+"threaded tree is\n");
    inOrder(root); 
}
}
//contributed by Arnab Kundu

Python3

# Python3 program to convert a Binary Tree to
# Threaded Tree
 
# A utility function to create a new node
class newNode:
    def __init__(self, key):
        self.left = self.right = None
        self.key = key
        self.isThreaded = None
         
# Converts tree with given root to threaded
# binary tree.
# This function returns rightmost child of
# root.
def createThreaded(root):
     
    # Base cases : Tree is empty or has 
    #               single node
    if root == None:
        return None
    if root.left == None and root.right == None:
        return root
 
    # Find predecessor if it exists
    if root.left != None:
         
        # Find predecessor of root (Rightmost
        # child in left subtree)
        l = createThreaded(root.left)
 
        # Link a thread from predecessor
        # to root.
        l.right = root
        l.isThreaded = True
 
    # If current node is rightmost child
    if root.right == None:
        return root
 
    # Recur for right subtree.
    return createThreaded(root.right)
 
# A utility function to find leftmost node
# in a binary tree rooted with 'root'.
# This function is used in inOrder()
def leftMost(root):
    while root != None and root.left != None:
        root = root.left
    return root
 
# Function to do inorder traversal of a
# threaded binary tree
def inOrder(root):
    if root == None:
        return
 
    # Find the leftmost node in Binary Tree
    cur = leftMost(root)
 
    while cur != None:
        print(cur.key, end = " ")
 
        # If this Node is a thread Node, then
        # go to inorder successor
        if cur.isThreaded:
            cur = cur.right
 
        else: # Else go to the leftmost child
              # in right subtree
            cur = leftMost(cur.right)
 
# Driver Code
if __name__ == '__main__':
     
    #         1
    #     / \
    #     2 3
    #     / \ / \
    #     4 5 6 7
    root = newNode(1)
    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(4)
    root.left.right = newNode(5)
    root.right.left = newNode(6)
    root.right.right = newNode(7)
 
    createThreaded(root)
 
    print("Inorder traversal of created",
                      "threaded tree is")
    inOrder(root)
 
# This code is contributed by PranchalK

C#

using System;
 
/* C# program to convert a Binary Tree to 
    Threaded Tree */
public class solution
{
 
 
/* structure of a node in threaded binary tree */
public class Node
{
    public int key;
    public Node left, right;
 
    // Used to indicate whether the right pointer 
    // is a normal right pointer or a pointer 
    // to inorder successor. 
    public bool isThreaded;
}
 
// Converts tree with given root to threaded 
// binary tree. 
// This function returns rightmost child of 
// root. 
public static Node createThreaded(Node root)
{
    // Base cases : Tree is empty or has single 
    //              node 
    if (root == null)
    {
        return null;
    }
    if (root.left == null && root.right == null)
    {
        return root;
    }
 
    // Find predecessor if it exists 
    if (root.left != null)
    {
        // Find predecessor of root (Rightmost 
        // child in left subtree) 
        Node l = createThreaded(root.left);
 
        // Link a thread from predecessor to 
        // root. 
        l.right = root;
        l.isThreaded = true;
    }
 
    // If current node is rightmost child 
    if (root.right == null)
    {
        return root;
    }
 
    // Recur for right subtree. 
    return createThreaded(root.right);
}
 
// A utility function to find leftmost node 
// in a binary tree rooted with 'root'. 
// This function is used in inOrder() 
public static Node leftMost(Node root)
{
    while (root != null && root.left != null)
    {
        root = root.left;
    }
    return root;
}
 
// Function to do inorder traversal of a threadded 
// binary tree 
public static void inOrder(Node root)
{
    if (root == null)
    {
        return;
    }
 
    // Find the leftmost node in Binary Tree 
    Node cur = leftMost(root);
 
    while (cur != null)
    {
        Console.Write(cur.key + " ");
 
        // If this Node is a thread Node, then go to 
        // inorder successor 
        if (cur.isThreaded)
        {
            cur = cur.right;
        }
 
        else // Else go to the leftmost child in right subtree
        {
            cur = leftMost(cur.right);
        }
    }
}
 
// A utility function to create a new node 
public static Node newNode(int key)
{
    Node temp = new Node();
    temp.left = temp.right = null;
    temp.key = key;
    return temp;
}
 
// Driver program to test above functions 
public static void Main(string[] args)
{
   /*       1 
            / \ 
           2   3 
          / \ / \ 
         4  5 6  7   */
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
    root.right.left = newNode(6);
    root.right.right = newNode(7);
 
    createThreaded(root);
 
    Console.WriteLine("Inorder traversal of created " + "threaded tree is\n");
    inOrder(root);
}
}
 
  // This code is contributed by Shrikant13

Javascript

<script>
/* javascript program to convert a Binary Tree to
    Threaded Tree */
   
/* structure of a node in threaded binary tree */
 class Node {
        constructor(val) {
            this.data = val;
            this.left = null;
            this.right = null;
     
   
    // Used to indicate whether the right pointer
    // is a normal right pointer or a pointer
    // to inorder successor.
    this.isThreaded = false;
    }
    }
 
   
// Converts tree with given root to threaded
// binary tree.
// This function returns rightmost child of
// root.
function createThreaded(root)
{
    // Base cases : Tree is empty or has single
    //              node
    if (root == null)
        return null;
    if (root.left == null &&
        root.right == null)
        return root;
   
    // Find predecessor if it exists
    if (root.left != null)
    {
        // Find predecessor of root (Rightmost
        // child in left subtree)
        var l = createThreaded(root.left);
   
        // Link a thread from predecessor to
        // root.
        l.right = root;
        l.isThreaded = true;
    }
   
    // If current node is rightmost child
    if (root.right == null)
        return root;
   
    // Recur for right subtree.
    return createThreaded(root.right);
}
   
// A utility function to find leftmost node
// in a binary tree rooted with 'root'.
// This function is used in inOrder()
function leftMost(root)
{
    while (root != null && root.left != null)
        root = root.left;
    return root;
}
   
// Function to do inorder traversal of a threadded
// binary tree
function inOrder(root)
{
    if (root == null) return;
   
    // Find the leftmost node in Binary Tree
    var cur = leftMost(root);
   
    while (cur != null)
    {
        document.write(cur.key + " ");
   
        // If this Node is a thread Node, then go to
        // inorder successor
        if (cur.isThreaded)
            cur = cur.right;
   
        else // Else go to the leftmost child in right subtree
            cur = leftMost(cur.right);
    }
}
   
// A utility function to create a new node
function newNode(key)
{
    var temp = new Node();
    temp.left = temp.right = null;
    temp.key = key;
    return temp;
}
   
// Driver program to test above functions
  
   /*       1
            / \
           2   3
          / \ / \
         4  5 6  7   */
    var root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
    root.right.left = newNode(6);
    root.right.right = newNode(7);
   
    createThreaded(root);
   
    document.write("Inorder traversal of created "+"threaded tree is<br/>");
    inOrder(root); 
 
// This code contributed by aashish1995
</script>

Output:

Inorder traversal of created threaded tree is
4 2 5 1 6 3 7

This algorithm works in O(n) time complexity and O(1) space other than function call stack.

This article is contributed by Gopal Agarwal. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

My Personal Notes

Related Articles

Table of Contents

Convert a Binary Tree to Threaded binary tree | Set 2 (Efficient)

C

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Start Your Coding Journey Now!