Teaching Learning based Optimization (TLBO)
Last Updated :
12 Apr, 2021
The process of finding optimal values for the specific parameters of a given system to fulfill all design requirements while considering the lowest possible cost is referred to as an optimization. Optimization problems can be found in all fields of science.
In general Optimization problem can be written as,
optimize 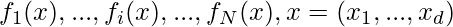
subject to,
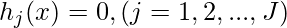
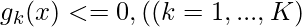
where 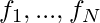 are the objectives, while
are the objectives, while 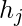 and
and 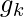 are the equality and inequality constraints, respectively. In the case when N=1, it is called single-objective optimization. When N≥2, it becomes a multi-objective optimization problem whose solution strategy is different from those for a single objective. This article mainly concerns single-objective optimization problems.
are the equality and inequality constraints, respectively. In the case when N=1, it is called single-objective optimization. When N≥2, it becomes a multi-objective optimization problem whose solution strategy is different from those for a single objective. This article mainly concerns single-objective optimization problems.
Many scholars and researchers have developed several meta heuristics to address complex/unsolved optimization problems. Example: Particle Swarm Optimization, Grey wolf optimization, Ant colony Optimization, Genetic Algorithms, Cuckoo search algorithm etc.
This article aims to introduce a novel meta-heuristic optimization technique called Teaching Learning Based Optimization (TLBO).
Inspiration of the algorithm:
Teaching learning-based optimization (TLBO) is a population-based meta-heuristic optimization technique that simulates the environment of a classroom to optimize a given objective function and it was proposed by R.V. Rao et al. in 2011.
In a classroom, the teacher puts his hard work and makes all the learners of a class educated. Then the learners interact with themselves to further modify and improve their gained knowledge.
This algorithm consists of two phases:
1) Teacher phase
All the students learn from teacher and gain knowledge
2) Learner phase
Students interact among themselves to share knowledge with each other
- Data structure to store students of class

Figure1: Data structure to store students
- Data structure to store ith student of the class

Figure2: Data structure to store ith student
Mathematical Model
1) Teaching phase
- Student with minimum fitness value is considered as teacher
- Xmean is used in this phase, where Xmean is the mean of all the students in the class
- New solution generation equation :
- Xnew = X + r*(Xteacher – TF*Xmean) ( 1)
- where TF is the teaching factor and is either 1 or 2 (chosen randomly)
- If Xnew is better than X. Then replace X with Xnew
2) Learner phase
- Xpartner: A randomly chosen fellow student from class
- Xpartner is chosen to interact and exchange knowledge
- New solution generation equation
- Let fitness of Xparter is Fpartner and that of X is F
- If(F < Fpartner ) ( 2)
- Xnew = X + r*(X – Xpartner )
- Else
- Xnew = X – r*(X – Xpartner)
- d. IF Xnew is better than X. Then replace X with Xnew
Algorithm
- Parameters of problem:
- Number of dimensions (d)
- Lower bound (minx)
- Upper bound (maxx)
- Hyperparameters of the algorithm:
- Number of particles (N)
- Maximum number of iterations (max_iter)
Step1: Randomly initialize Class of N students Xi ( i=1, 2, …, n)
Step2: Compute fitness value of all the students
Step3: For Iter in range(max_iter): # loop max_iter times
For i in range(N): # for each student
# Teaching phase-----------
Xteacher = student with least fitness value
Xmean = mean of all the students
TF ( teaching factor) = either 1 or 2 ( randomly chosen )
Xnew = class[i].position + r*(Xteacher - TF*Xmean)
# if Xnew < minx OR Xnew > maxx then clip it
Xnew = min(Xnew, minx)
Xnew = max(Xnew, maxx)
# compute fitness of new solution
fnew = fitness(Xnew)
# greedy selection strategy
if(fnew < class[i].fitness)
class[i].position = Xnew
class[i].fitness = fnew
# Learning phase------------
Xpartner = randomly chosen student from class
if(class[i].fitness < Xpartner.fitness):
Xnew = class[i].position + r*(class[i].position - Xpartner)
else
Xnew = class[i].position - r*(class[i].position - Xpartner)
# if Xnew < minx OR Xnew > maxx then clip it
Xnew = min(Xnew, minx)
Xnew = max(Xnew, maxx)
# compute fitness of new solution
fnew = fitness(Xnew)
# greedy selection strategy
if(fnew < class[i].fitness)
class[i].position = Xnew
class[i].fitness = fnew
End-for
End -for
Step 4: Return best student from class
Share your thoughts in the comments
Please Login to comment...