Square free semiprimes in a given range using C++ STL
Last Updated :
21 Aug, 2019
Given two integers
L and
R (L < = R). The task is to find all square free
semiprimes in the range L to R (both inclusive).
Examples:
Input : L = 1, R = 10
Output : 2
4, 6, 9, 10 are semi primes. But 6, 10 are square free semi primes.
Input : L = 10, R = 20
Output : 3
Prerequisites: Sieve of Eratosthenes,
upper and lower bound
Understanding :
Semiprimes are numbers of the form
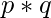
where p and q are primes, not necessarily distinct. All semiprime
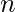
has only 4 factors
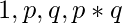
where p and q are the only two prime factors and
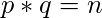
.
Naive Approach:
Precompute all prime number upto
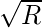
. Find all combinations of two prime
p and
q such that
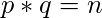
is between
L and
R. Iterating through all combinations of prime would give a time complexity of
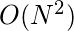
. This solution, however, will not work for large
L and
R values.
Time Complexity: O(N^2)
Efficient Approach:
Precompute all prime number up to
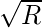
. We can divide the problem of finding two primes p and q into a simpler form.
As
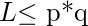
we can say that
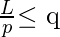
. Similarly as
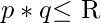
we can say that
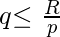
.
Now the problem is reduced to finding the count of q such that
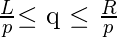
for all p.
Here, we can use binary search for finding
upper_bound of
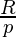
from list of prime numbers and subtract it from index of
lower_bound of
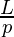
from list of prime numbers to find the count of all
q in range
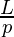
to
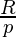
for the given
p. Repeating the above step for all prime
p will give the answer for given range
L to
R
Below is the implementation of the above approach :
#include <bits/stdc++.h>
using namespace std;
#define N 78498
void Sieve(int pre[])
{
int MX = 1e6;
bool prime[MX + 1];
int i = 2;
int idx = 0;
memset(prime, true, sizeof(prime));
for (i = 2; i <= MX; i++)
{
if (prime[i])
{
pre[idx++] = i;
for (int j = (i << 1); j <= MX; j += i)
prime[j] = false;
}
}
}
int semiPrimeCount(int L, int R)
{
int pre[N];
Sieve(pre);
int res = 0;
int j = 1;
for (auto p : pre) {
int ub_num = R / p;
auto ub = upper_bound(pre + j, pre + N, ub_num);
int lb_num = (L / p) + ((L % p) > 0);
auto lb = lower_bound(pre + j, pre + N, lb_num);
res += ub - lb;
j++;
if (p * p >= R)
break;
}
return res;
}
int main()
{
int L = 10, R = 20;
cout << semiPrimeCount(L, R);
return 0;
}
|
Time Complexity: O(N*logN)
Share your thoughts in the comments
Please Login to comment...