Probability of getting a perfect square when a random number is chosen in a given range

Given two integers L and R that denote a range, the task is to find the probability of getting a perfect square number when a random number is chosen in the range L to R.

Examples:

Input: L = 6, R = 20 
Output: 0.133333 
Explanation:
Perfect squares in range [6, 20] = {9, 16} => 2 perfect squares 
Total numbers in range [6, 20] = 15 
Probability = 2 / 15 = 0.133333

Input: L = 16, R = 25 
Output: 0.2 

Approach: The key observation in this problem is the count of the perfect squares in the range from 0 to a number can be computed with the given formulae: 

// Count of perfect squares in the range 0 to N is given as 
Count of perfect squares = Floor(sqrt(N)) 

Similarly, the count of the perfect squares in the given range can be computed with the help of the above formulae as follows: 

Count of perfect Squares[L, R] = floor(sqrt(R)) – ceil(sqrt(L)) + 1 
Total numbers in the range = R – L + 1

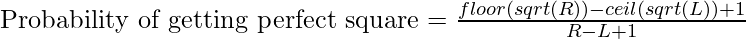
Below is the implementation of the above approach: 

C++

// C++ implementation to find the
// probability of getting a
// perfect square number

#include <bits/stdc++.h>
using namespace std;

// Function to return the probability
// of getting a perfect square
// number in a range
float findProb(int l, int r)
{
    // Count of perfect squares
    float countOfPS = floor(sqrt(r)) - ceil(sqrt(l)) + 1;

    // Total numbers in range l to r
    float total = r - l + 1;

    // Calculating probability
    float prob = (float)countOfPS / (float)total;
    return prob;
}

// Driver Code
int main()
{
    int L = 16, R = 25;
    cout << findProb(L, R);

    return 0;
}

Java

// Java implementation to find the
// probability of getting a
// perfect square number

class GFG{

// Function to return the probability
// of getting a perfect square
// number in a range
static float findProb(int l, int r)
{

    // Count of perfect squares
    float countOfPS = (float) (Math.floor(Math.sqrt(r)) -
                               Math.ceil(Math.sqrt(l)) + 1);

    // Total numbers in range l to r
    float total = r - l + 1;

    // Calculating probability
    float prob = (float)countOfPS / (float)total;
    return prob;
}

// Driver Code
public static void main(String[] args)
{
    int L = 16, R = 25;
    System.out.print(findProb(L, R));
}
}

// This code is contributed by Amit Katiyar

Python3

# Python3 implementation to find
# the probability of getting a
# perfect square number
import math

# Function to return the probability
# of getting a perfect square
# number in a range
def findProb(l, r):

    # Count of perfect squares
    countOfPS = (math.floor(math.sqrt(r)) -
                  math.ceil(math.sqrt(l)) + 1)

    # Total numbers in range l to r
    total = r - l + 1

    # Calculating probability
    prob = countOfPS / total

    return prob

# Driver code
if __name__=='__main__':

    L = 16
    R = 25

    print(findProb(L, R))

# This code is contributed by rutvik_56

C#

// C# implementation to find the probability
// of getting a perfect square number
using System;

class GFG{

// Function to return the probability
// of getting a perfect square
// number in a range
static float findProb(int l, int r)
{

    // Count of perfect squares
    float countOfPS = (float)(Math.Floor(Math.Sqrt(r)) -
                            Math.Ceiling(Math.Sqrt(l)) + 1);

    // Total numbers in range l to r
    float total = r - l + 1;

    // Calculating probability
    float prob = (float)countOfPS / (float)total;
    return prob;
}

// Driver Code
public static void Main(String[] args)
{
    int L = 16, R = 25;

    Console.Write(findProb(L, R));
}
}

// This code is contributed by Amit Katiyar

Javascript

<script>

// Javascript implementation to find the
// probability of getting a
// perfect square number

// Function to return the probability
// of getting a perfect square
// number in a range
function findProb(l, r)
{

    // Count of perfect squares
    var countOfPS = (Math.floor(Math.sqrt(r)) -
                     Math.ceil(Math.sqrt(l)) + 1);

    // Total numbers in range l to r
    var total = r - l + 1;

    // Calculating probability
    var prob = countOfPS / total;
    return prob;
}

// Driver code
var L = 16, R = 25;

// Function Call
document.write(findProb(L, R));

// This code is contributed by Khushboogoyal499

</script>

Output:

0.2

Time Complexity: O(log(r) + log(l))
 Auxiliary Space: O(1)