Spelling Correction using K-Gram Overlap
Last Updated :
02 Aug, 2019
While the minimum edit distance discussed in this
article provides a good list of possibly correct words, there are far too many words in the English dictionary to consider finding the edit distance between all pairs. To simplify the list of candidate words, the k-gram overlap is used in typical IR and NLP systems.
K-Grams
K-grams are k-length subsequences of a string. Here, k can be 1, 2, 3 and so on. For k=1, each resulting subsequence is called a “unigram”; for k=2, a “bigram”; and for k=3, a “trigram”. These are the most widely used k-grams for spelling correction, but the value of k really depends on the situation and context.
As an example, consider the string “catastrophic”. In this case,
- Unigrams: [“c”, “a”, “t”, “a”, “s”, “t”, “r”, “o”, “p”, “h”, “i”, “c”]
- Bigrams: [“ca”, “at”, “ta”, “as”, “st”, “tr”, “ro”, “op”, “ph”, “hi”, “ic”]
- Trigrams: [“cat”, “ata”, “tas”, “ast”, “str”, “tro”, “rop”, “oph”, “phi”, “hic”]
K-Gram Index
A k-gram index maps a k-gram to a postings list of all possible vocabulary terms that contain it. The figure below shows the k-gram postings list corresponding to the bigram “ur”.

It is noteworthy that the postings list is sorted alphabetically.
Spelling Correction
While creating the candidate list of possible corrected words, we can use the “k-gram overlap” to find the most likely corrections.
Consider the misspelt word: “appe”. The postings lists for the bigrams contained in it are shown below. Note that these are only sample subsets of the postings lists; the actual postings list would, of course, contain thousands of words in them.

To find the k-gram overlap between two postings list, we use the Jaccard coefficient. Here, A and B are two sets (postings lists), A for the misspelt word and B for the corrected word.

Now, consider some candidate terms for spelling correction, namely “ape” and “apple”.
“ape”
To find the
Jaccard coefficient, simply scan through the postings lists of all bigrams of “appe” and count the instances where “ape” appears.
In the first postings list, “ape” appears 1 time. In the second postings list, “ape” appears 0 times. In the third postings list, “ape” appears 1 time. Therefore,
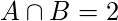
. Now, the no. of bigrams in “appe” is 3, and the no. of bigrams in “ape” is 2. Therefore,
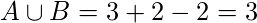
.
J(A, B) = 2/3 = 0.67.
“apple”
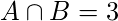
. Now, the no. of bigrams in “appe” is 3, and the no. of bigrams in “apple” is 4. Therefore,
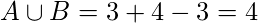
.
J(A, B) = 3/4 = 0.75.
This suggests that “apple” is a more plausible correction. Practically, this method is used to filter out unlikely corrections.
The steps involved for spelling correction are:
- Find the k-grams of the misspelled word.
- For each k-gram, linearly scan through the postings list in the k-gram index.
- Find k-gram overlaps after having linearly scanned the lists (no extra time complexity because we are finding the Jaccard coefficient).
- Return the terms with the maximum k-gram overlaps.
Share your thoughts in the comments
Please Login to comment...