Serialize and Deserialize a Binary Tree

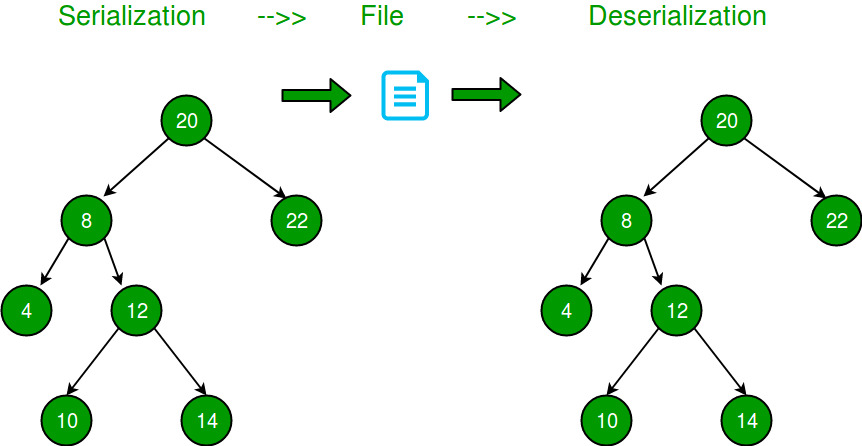
Serialization is to store the tree in a file so that it can be later restored. The structure of the tree must be maintained. Deserialization is reading the tree back from a file.

Following are some simpler versions of the problem:

If given Tree is a Binary Search Tree?

If the given Binary Tree is Binary Search Tree, we can store it by either storing preorder or postorder traversal. In case of Binary Search Trees, only preorder or postorder traversal is sufficient to store structure information. 

If given Binary Tree is Complete Tree?

A Binary Tree is complete if all levels are completely filled except possibly the last level and all nodes of last level are as left as possible (Binary Heaps are complete Binary Tree). For a complete Binary Tree, level order traversal is sufficient to store the tree. We know that the first node is root, next two nodes are nodes of next level, next four nodes are nodes of 2nd level and so on. 

If given Binary Tree is Full Tree?

A full Binary is a Binary Tree where every node has either 0 or 2 children. It is easy to serialize such trees as every internal node has 2 children. We can simply store preorder traversal and store a bit with every node to indicate whether the node is an internal node or a leaf node.

How to store a general Binary Tree?

A simple solution is to store both Inorder and Preorder traversals. 

This solution requires space twice the size of the Binary Tree. We can save space by storing Preorder traversal and a marker for NULL pointers. 

• Store all possible child nodes for each node.
• If there is no child node then push -1 for that child.
• Put this preorder traversal in the file.

Examples:

Input:
     12
    /
13
Output: 12 13 -1 -1 -1

Input:
      20
    /   \
8     22 
Output: 20 8 -1 -1 22 -1 -1 

Input:
         20
       /    
     8     
   /  \
4   12 
    /   \
10  14
Output: 20 8 4 -1 -1 12 10 -1 -1 14 -1 -1 -1 

Input:
            20
           /    
         8     
       /
   10
  /
5
Output: 20 8 10 5 -1 -1 -1 -1 -1 

Input:
          20
            \
             8
              \   
               10
                 \
                  5   

Output: 20 -1 8 -1 10 -1 5 -1 -1

How to deserialize the above serialization?

Deserialization can be done by simply reading data from the file one by one and keep on adding children till a -1 is reached. If both the children are NULL then return back to the parent.

Below is the implementation of the above idea.

C++

// A C++ program to demonstrate serialization and
// deserialization of Binary Tree

#include <bits/stdc++.h>
using namespace std;

#define MARKER -1

// A binary tree Node has key,
// pointer to left and right children
struct Node {
    int key;
    struct Node *left, *right;
};

// Helper function that allocates a new Node with the
// given key and NULL left and right pointers.
struct Node* newNode(int key)
{
    struct Node* temp = new Node();
    temp->key = key;
    temp->left = temp->right = NULL;
    return (temp);
}

// This function stores a tree in a file pointed by fp
void serialize(Node* root, FILE* fp)
{
    // If current node is NULL, store marker
    if (root == NULL) {
        fprintf(fp, "%d ", MARKER);
        return;
    }

    // Else, store current node and
    // recur for its children
    fprintf(fp, "%d ", root->key);
    serialize(root->left, fp);
    serialize(root->right, fp);
}

// This function constructs a tree from
// a file pointed by 'fp'
void deSerialize(Node*& root, FILE* fp)
{
    // Read next item from file.
    // If there are no more items
    // or next item is marker, then return
    int val;
    if (!fscanf(fp, "%d ", &val) || val == MARKER)
        return;

    // Else create node with this item
    // and recur for children
    root = newNode(val);
    deSerialize(root->left, fp);
    deSerialize(root->right, fp);
}

// A simple inorder traversal used for
// testing the constructed tree
void inorder(Node* root)
{
    if (root) {
        inorder(root->left);
        printf("%d ", root->key);
        inorder(root->right);
    }
}

// Driver code
int main()
{
    // Construct a tree shown in the above figure
    struct Node* root = newNode(20);
    root->left = newNode(8);
    root->right = newNode(22);
    root->left->left = newNode(4);
    root->left->right = newNode(12);
    root->left->right->left = newNode(10);
    root->left->right->right = newNode(14);

    // Open a file and serialize the tree into the file
    FILE* fp = fopen("tree.txt", "w");
    if (fp == NULL) {
        puts("Could not open file");
        return 0;
    }
    serialize(root, fp);
    fclose(fp);

    // Deserialize the stored tree into root1
    Node* root1 = NULL;
    fp = fopen("tree.txt", "r");
    deSerialize(root1, fp);

    printf("Inorder Traversal of the tree constructed from "
           "file:\n");
    inorder(root1);

    return 0;
}

Java

// A Java program to demonstrate serialization and
// deserialization of Binary Tree

import java.util.*;

// A binary tree Node has key,
// pointer to left and right children
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

class BinaryTree {
    TreeNode root;

    // Encodes a tree to a single string.
    public static String serialize(TreeNode root)
    {
        if (root == null) {
            return null;
        }
        Stack<TreeNode> s = new Stack<>();
        s.push(root);

        List<String> l = new ArrayList<>();
        while (!s.isEmpty()) {
            TreeNode t = s.pop();

            // If current node is NULL, store marker
            if (t == null) {
                l.add("#");
            }
            else {

                // Else, store current node
                // and recur for its children
                l.add("" + t.val);
                s.push(t.right);
                s.push(t.left);
            }
        }
        return String.join(",", l);
    }

    static int t;

    // Decodes your encoded data to tree.
    public static TreeNode deserialize(String data)
    {
        if (data == null)
            return null;
        t = 0;
        String[] arr = data.split(",");
        return helper(arr);
    }

    public static TreeNode helper(String[] arr)
    {
        if (arr[t].equals("#"))
            return null;

        // Create node with this item
        // and recur for children
        TreeNode root
            = new TreeNode(Integer.parseInt(arr[t]));
        t++;
        root.left = helper(arr);
        t++;
        root.right = helper(arr);
        return root;
    }

    // A simple inorder traversal used
    // for testing the constructed tree
    static void inorder(TreeNode root)
    {
        if (root != null) {
            inorder(root.left);
            System.out.print(root.val + " ");
            inorder(root.right);
        }
    }

    // Driver code
    public static void main(String args[])
    {
        // Construct a tree shown in the above figure
        BinaryTree tree = new BinaryTree();
        tree.root = new TreeNode(20);
        tree.root.left = new TreeNode(8);
        tree.root.right = new TreeNode(22);
        tree.root.left.left = new TreeNode(4);
        tree.root.left.right = new TreeNode(12);
        tree.root.left.right.left = new TreeNode(10);
        tree.root.left.right.right = new TreeNode(14);

        String serialized = serialize(tree.root);
        System.out.println("Serialized view of the tree:");
        System.out.println(serialized);
        System.out.println();

        // Deserialize the stored tree into root1
        TreeNode t = deserialize(serialized);

        System.out.println(
            "Inorder Traversal of the tree constructed"
            + " from serialized String:");
        inorder(t);
    }
}

C#

// C# code for the above approach
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int x) { val = x; }
}

class BinaryTree {
    public TreeNode root;

    // Encodes a tree to a single string.
    public static string Serialize(TreeNode root)
    {
        if (root == null) {
            return null;
        }
        Stack<TreeNode> s = new Stack<TreeNode>();
        s.Push(root);

        List<string> l = new List<string>();
        while (s.Count > 0) {
            TreeNode t = s.Pop();

            // If current node is NULL, store marker
            if (t == null) {
                l.Add("#");
            }
            else {

                // Else, store current node
                // and recur for its children
                l.Add(t.val.ToString());
                s.Push(t.right);
                s.Push(t.left);
            }
        }
        return string.Join(",", l);
    }

    static int t;

    // Decodes your encoded data to tree.
    public static TreeNode Deserialize(string data)
    {
        if (data == null)
            return null;
        t = 0;
        string[] arr = data.Split(',');
        return Helper(arr);
    }

    public static TreeNode Helper(string[] arr)
    {
        if (arr[t].Equals("#"))
            return null;

        // Create node with this item
        // and recur for children
        TreeNode root = new TreeNode(int.Parse(arr[t]));
        t++;
        root.left = Helper(arr);
        t++;
        root.right = Helper(arr);
        return root;
    }

    // A simple inorder traversal used
    // for testing the constructed tree
    static void Inorder(TreeNode root)
    {
        if (root != null) {
            Inorder(root.left);
            Console.Write(root.val + " ");
            Inorder(root.right);
        }
    }

    // Driver code
    public static void Main(string[] args)
    {
        // Construct a tree shown in the above figure
        BinaryTree tree = new BinaryTree();
        tree.root = new TreeNode(20);
        tree.root.left = new TreeNode(8);
        tree.root.right = new TreeNode(22);
        tree.root.left.left = new TreeNode(4);
        tree.root.left.right = new TreeNode(12);
        tree.root.left.right.left = new TreeNode(10);
        tree.root.left.right.right = new TreeNode(14);

        string serialized = Serialize(tree.root);
        Console.WriteLine("Serialized view of the tree:");
        Console.WriteLine(serialized);
        Console.WriteLine();

        // Deserialize the// stored tree into root1
        TreeNode t = Deserialize(serialized);

        Console.WriteLine(
            "Inorder Traversal of the tree constructed"
            + " from serialized String:");
        Inorder(t);
    }
}

// This code is contributed by Potta Lokesh

Javascript

// A JavaScript program to demonstrate serialization and
// deserialization of Binary Tree

// Define the marker value
const MARKER = -1;

// A binary tree Node has key,
// pointer to left and right children
class Node {
    constructor(key) {
        this.key = key;
        this.left = null;
        this.right = null;
    }
}

// Helper function that allocates a new Node with the
// given key and NULL left and right pointers.
function newNode(key) {
    let temp = new Node(key);
    return temp;
}

// This function stores a tree in a file pointed by fp
function serialize(root, fp) {
    // If current node is NULL, store marker
    if (root === null) {
        fp.push(MARKER);
        return;
    }

    // Else, store current node and
    // recur for its children
    fp.push(root.key);
    serialize(root.left, fp);
    serialize(root.right, fp);
}

// This function constructs a tree from
// a file pointed by 'fp'
function deSerialize(root, fp) {
    // Read next item from file.
    // If there are no more items
    // or next item is marker, then return
    let val = fp.shift();
    if (val === undefined || val === MARKER) {
        return null;
    }

    // Else create node with this item
    // and recur for children
    root = newNode(val);
    root.left = deSerialize(root.left, fp);
    root.right = deSerialize(root.right, fp);
    return root;
}

// A simple inorder traversal used for
// testing the constructed tree
function inorder(root) {
    if (root) {
        inorder(root.left);
        console.log(root.key);
        inorder(root.right);
    }
}

// Driver code
function main() {
    // Construct a tree shown in the above figure
    let root = newNode(20);
    root.left = newNode(8);
    root.right = newNode(22);
    root.left.left = newNode(4);
    root.left.right = newNode(12);
    root.left.right.left = newNode(10);
    root.left.right.right = newNode(14);

    // Open a file and serialize the tree into the file
    let fp = [];
    serialize(root, fp);

    // Deserialize the stored tree into root1
    let root1 = null;
    root1 = deSerialize(root1, fp);

    console.log("Inorder Traversal of the tree constructed from file:");
    inorder(root1);

    return 0;
}

main();

Python3

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class BinaryTree:
    def __init__(self):
        self.root = None

    # Encodes a tree to a single string.
    def serialize(self, root):
        if not root:
            return None

        stack = [root]
        l = []

        while stack:
            t = stack.pop()

            # If current node is NULL, store marker
            if not t:
                l.append("#")
            else:
                # Else, store current node
                # and recur for its children
                l.append(str(t.val))
                stack.append(t.right)
                stack.append(t.left)

        return ",".join(l)

    # Decodes your encoded data to tree.
    def deserialize(self, data):
        if not data:
            return None

        global t
        t = 0
        arr = data.split(",")
        return self.helper(arr)

    def helper(self, arr):
        global t
        if arr[t] == "#":
            return None

        # Create node with this item
        # and recur for children
        root = TreeNode(int(arr[t]))
        t += 1
        root.left = self.helper(arr)
        t += 1
        root.right = self.helper(arr)
        return root

    # A simple inorder traversal used
    # for testing the constructed tree
    def inorder(self, root):
        if root:
            self.inorder(root.left)
            print(root.val, end=" ")
            self.inorder(root.right)

# Driver code
if __name__ == '__main__':
    # Construct a tree shown in the above figure
    tree = BinaryTree()
    tree.root = TreeNode(20)
    tree.root.left = TreeNode(8)
    tree.root.right = TreeNode(22)
    tree.root.left.left = TreeNode(4)
    tree.root.left.right = TreeNode(12)
    tree.root.left.right.left = TreeNode(10)
    tree.root.left.right.right = TreeNode(14)

    serialized = tree.serialize(tree.root)
    print("Serialized view of the tree:")
    print(serialized)
    print()

    # Deserialize the stored tree into root1
    t = tree.deserialize(serialized)

    print("Inorder Traversal of the tree constructed from serialized String:")
    tree.inorder(t)

How much extra space is required in above solution?

If there are n keys, then the above solution requires n+1 markers which may be better than simple solution (storing keys twice) in situations where keys are big or keys have big data items associated with them.

Can we optimize it further?

The above solution can be optimized in many ways. If we take a closer look at the above serialized trees, we can observe that all leaf nodes require two markers. One simple optimization is to 

• Store a separate bit with every node to indicate that the node is internal or external. 
• This way we don’t have to store two markers with every leaf node as leaves can be identified by the extra bit. 
• We still need a marker for internal nodes with one child. 

For example, in the following diagram, the character ‘ is used to indicate an internal node set bit, and ‘/‘ is used as NULL marker.

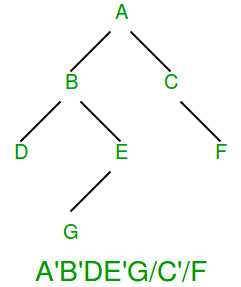
Please note that there are always more leaf nodes than internal nodes in a Binary Tree (Number of the leaf nodes is the number of internal nodes (with degree 2) plus 1, so this optimization makes sense.

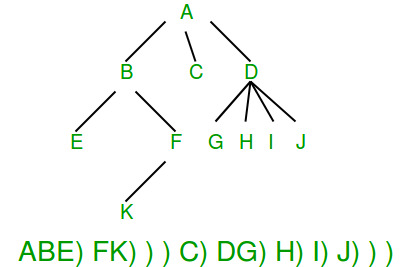
How to serialize N-ary tree?

In an N-ary tree, there is no designated left or right child. We can store an ‘end of children‘ marker with every node. The following diagram shows serialization where ‘)’ is used as the end of the children marker. We will soon be covering implementation for N-ary tree.