Root to leaf path sum equal to a given number

Given a binary tree and a number, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals the given number. Return false if no such path can be found. 

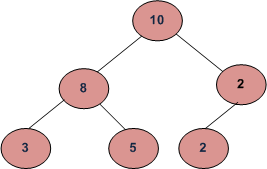
Example:

Input:      10          Sum = 23
              /     \
           8        2
        /    \     /
      3      5  2

Output: True 
Explanation:  Root to leaf path sum, existing in this tree are
21 –> 10 – 8 – 3 
23 –> 10 – 8 – 5 
14 –> 10 – 2 – 2
So it is possible to get sum = 23

Recursively move to left and right subtree and decrease sum by the value of the current node and if at any point the current node is equal to a leaf node and remaining sum is equal to zero then the answer is true

Follow the given steps to solve the problem using the above approach:

• Recursively move to the left and right subtree and at each call decrease the sum by the value of the current node
• If at any level the current node is a leaf node and the remaining sum is equal to zero then return true

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

#define bool int

/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node {
public:
    int data;
    node* left;
    node* right;
};

/*
Given a tree and a sum, return true if there is a path from
the root down to a leaf, such that adding up all the values
along the path equals the given sum.

Strategy: subtract the node value from the sum when
recurring down, and check to see if the sum is 0 when you
when you reach the leaf node.
*/
bool hasPathSum(node* Node, int sum)
{
    if (Node == NULL)
        return 0;

    bool ans = 0;

    int subSum = sum - Node->data;

    /* If we reach a leaf node and sum becomes 0 then return
     * true*/
    if (subSum == 0 && Node->left == NULL
        && Node->right == NULL)
        return 1;

    /* otherwise check both subtrees */
    if (Node->left)
        ans = ans || hasPathSum(Node->left, subSum);
    if (Node->right)
        ans = ans || hasPathSum(Node->right, subSum);

    return ans;
}

/* UTILITY FUNCTIONS */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newnode(int data)
{
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;

    return (Node);
}

// Driver's Code
int main()
{

    int sum = 21;

    /* Constructed binary tree is
                10
            / \
            8 2
        / \ /
        3 5 2
    */
    node* root = newnode(10);
    root->left = newnode(8);
    root->right = newnode(2);
    root->left->left = newnode(3);
    root->left->right = newnode(5);
    root->right->left = newnode(2);

      // Function call
    if (hasPathSum(root, sum))
        cout << "There is a root-to-leaf path with sum "
             << sum;
    else
        cout << "There is no root-to-leaf path with sum "
             << sum;

    return 0;
}

// This code is contributed by rathbhupendra

C

// C program for the above approach

#include <stdio.h>
#include <stdlib.h>
#define bool int

/* A binary tree node has data, pointer to left child
   and a pointer to right child */
struct node {
    int data;
    struct node* left;
    struct node* right;
};

/*
 Given a tree and a sum, return
 true if there is a path from
 the root down to a leaf, such
 that adding up all the values
 along the path equals the given sum.

 Strategy: subtract the node
 value from the sum when
 recurring down, and check to
 see if the sum is 0 when you reach the leaf node.
*/
bool hasPathSum(struct node* node, int sum)
{
    if (node == NULL)
        return 0;
    bool ans = 0;

    int subSum = sum - node->data;

    /* If we reach a leaf node
          and sum becomes 0 then
           * return true*/
    if (subSum == 0 && node->left == NULL
        && node->right == NULL)
        return 1;

    /* otherwise check both subtrees */
    if (node->left)
        ans = ans || hasPathSum(node->left, subSum);
    if (node->right)
        ans = ans || hasPathSum(node->right, subSum);

    return ans;
}

/* UTILITY FUNCTIONS */
/* Helper function that
   allocates a new node with the
   given data and NULL left
   and right pointers. */
struct node* newnode(int data)
{
    struct node* node
        = (struct node*)malloc(sizeof(struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;

    return (node);
}

// Driver's Code
int main()
{

    int sum = 21;

    /* Constructed binary tree is
              10
            /   \
          8      2
        /  \    /
      3     5  2
    */
    struct node* root = newnode(10);
    root->left = newnode(8);
    root->right = newnode(2);
    root->left->left = newnode(3);
    root->left->right = newnode(5);
    root->right->left = newnode(2);

    // Function call
    if (hasPathSum(root, sum))
        printf("There is a root-to-leaf path with sum %d",
               sum);
    else
        printf("There is no root-to-leaf path with sum %d",
               sum);

    getchar();
    return 0;
}

Java

// Java program to print
// root to leaf path sum
// equal to a given number

/* A binary tree node has data,
 pointer to left child
   and a pointer to right child */
class Node {
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class BinaryTree {

    Node root;

    /*
     Given a tree and a sum,
     return true if there is a path
     from the root down to a leaf,
     such that adding up all
     the values along the path
     equals the given sum.

     Strategy: subtract the node
     value from the sum when
     recurring down, and check to
     see if the sum is 0 you reach the leaf node.
     */

    boolean hasPathSum(Node node, int sum)
    {
        /* If the tree is empty there is no way the reqd sum
         * will be there. */
        if (root == null)
            return false;
        boolean ans = false;
        int subSum = sum - node.data;
        if (subSum == 0 && node.left == null
            && node.right == null)
            return (ans = true);
        if (node.left != null)

            // ans || hasPathSum... has no utility if the
            // ans is false
            ans = ans || hasPathSum(node.left, subSum);

        if (node.right != null)

            // But if it is true then we can avoid calling
            // hasPathSum here as answer has already been
            // found
            ans = ans || hasPathSum(node.right, subSum);
        return (ans);
    }

    // Driver's Code
    public static void main(String args[])
    {
        int sum = 21;

        /* Constructed binary tree is
              10
             /  \
           8     2
          / \   /
         3   5 2
        */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(8);
        tree.root.right = new Node(2);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(2);

          // Function call
        if (tree.hasPathSum(tree.root, sum))
            System.out.println(
                "There is a root to leaf path with sum "
                + sum);
        else
            System.out.println(
                "There is no root to leaf path with sum "
                + sum);
    }
}

// This code has been contributed by Mayank
// Jaiswal(mayank_24)

Python3

# Python3 program to find if
# there is a root to sum path

# A binary tree node


class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


"""
 Given a tree and a sum, return
 true if there is a path from the root
 down to a leaf, such that
 adding up all the values along the path
 equals the given sum.

 Strategy: subtract the node
 value from the sum when recurring down,
 and check to see if the sum
 is 0 when you run out of tree.
"""
# s is the sum


def hasPathSum(node, s):
    ans = 0
    subSum = s - node.data

    # If we reach a leaf node and sum becomes 0, then
    # return True
    if(subSum == 0 and node.left == None and node.right == None):
        return True

    # Otherwise check both subtrees
    if node.left is not None:
        ans = ans or hasPathSum(node.left, subSum)
    if node.right is not None:
        ans = ans or hasPathSum(node.right, subSum)

    return ans

# Driver's Code
if __name__ == "__main__":
    s = 21
    root = Node(10)
    root.left = Node(8)
    root.right = Node(2)
    root.left.right = Node(5)
    root.left.left = Node(3)
    root.right.left = Node(2)

    # Function call
    if hasPathSum(root, s):
        print("There is a root-to-leaf path with sum %d" % (s))
    else:
        print("There is no root-to-leaf path with sum %d" % (s))

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// C# program to print root to
// leaf path sum equal to a given number
using System;

/* A binary tree node has data, pointer
to left child and a pointer to right child */
public class Node {
    public int data;
    public Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class GFG {
    public Node root;

    /*
    Given a tree and a sum, return true if
    there is a path from the root down to a
    leaf, such that adding up all the values
    along the path equals the given sum.

    Strategy: subtract the node value from the
    sum when recurring down, and check to see
    if the sum is 0 when you you reach the leaf node..
    */

    public virtual bool haspathSum(Node node, int sum)
    {
        ans = false;

        int subsum = sum - node.data;
        if (subsum == 0 && node.left == null
            && node.right == null) {
            return true;
        }

        /* otherwise check both subtrees */
        if (node.left != null) {
            ans = ans || haspathSum(node.left, subsum);
        }
        if (node.right != null) {
            ans = ans || haspathSum(node.right, subsum);
        }
        return ans;
    }

    // Driver's Code
    public static void Main(string[] args)
    {
        int sum = 21;

        /* Constructed binary tree is
            10
            / \
        8     2
        / \ /
        3 5 2
        */
        GFG tree = new GFG();
        tree.root = new Node(10);
        tree.root.left = new Node(8);
        tree.root.right = new Node(2);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(2);

          // Function call
        if (tree.haspathSum(tree.root, sum)) {
            Console.WriteLine("There is a root to leaf "
                              + "path with sum " + sum);
        }
        else {
            Console.WriteLine("There is no root to leaf "
                              + "path with sum " + sum);
        }
    }
}

// This code is contributed by Shrikant13

Javascript

// javascript program to print
// root to leaf path sum
// equal to a given number

/* A binary tree node has data,
 pointer to left child
   and a pointer to right child */

class Node {
        constructor(val) {
            this.data = val;
            this.left = null;
            this.right = null;
        }
    }

var root;

    /*
     Given a tree and a sum,
     return true if there is a path
     from the root down to a leaf,
     such that adding up all
     the values along the path
     equals the given sum.

     Strategy: subtract the node
     value from the sum when
     recurring down, and check to
     see if the sum is 0 you reach the leaf node.
     */

    function hasPathSum(node , sum)
    {
      var ans = false;
      var subSum = sum - node.data;
      if(subSum == 0 && node.left == null && node.right == null)
        return(ans = true);
      if(node.left != null)

        // ans || hasPathSum... has no utility if the ans is false
        ans = ans || hasPathSum(node.left, subSum);

      if(node.right != null)

        // But if it is true then we can afunction calling hasPathSum
        // here as answer has already been found
        ans = ans || hasPathSum(node.right, subSum);
      return(ans);
    }

    // Driver Code

        var sum = 21;

        /* Constructed binary tree is
              10
             /  \
           8     2
          / \   /
         3   5 2
        */

        var root = new Node(10);
        root.left = new Node(8);
        root.right = new Node(2);
        root.left.left = new Node(3);
        root.left.right = new Node(5);
        root.right.left = new Node(2);

        if (hasPathSum(root, sum))
            document.write(
                "There is a root to leaf path with sum "
                + sum);
        else
            document.write(
                "There is no root to leaf path with sum "
                + sum);

// This code is contributed by gauravrajput1

Output

There is a root-to-leaf path with sum 21

Time Complexity: O(N)

Space Complexity: O(N) or O(H)

Approach 2: Iterative Approach using Stack
In this approach, we use a stack to perform a preorder traversal of the binary tree. We maintain two stacks – one to store the nodes and another to store the sum of values along the path to that node. Whenever we encounter a leaf node, we check if the sum matches the target sum. If it does, we return true, otherwise, we continue traversing the tree.

• Check if the root node is NULL. If it is, return false, since there is no path to follow.
• Create two stacks, one for the nodes and one for the sums. Push the root node onto the node stack and its data onto the sum stack.
• While the node stack is not empty, do the following:
  • Pop a node from the node stack and its corresponding sum from the sum stack.
  •  Check if the node is a leaf node (i.e., it has no left or right child). If it is, check if the sum equals the target sum. If it does, return true, since we have found a path that adds up to the target sum.
  •  If the node has a left child, push it onto the node stack and push the sum plus the left child’s data onto the sum stack.
  • If the node has a right child, push it onto the node stack and push the sum plus the right child’s data onto the sum stack.
• If we reach this point, it means we have exhausted all paths and haven’t found any that add up to the target sum. Return false.

C++

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int data;
    Node* left, *right;
    Node(int val) {
        data = val;
        left = right = NULL;
    }
};

bool hasPathSum(Node* root, int targetSum) {
    if (root == NULL) return false;
    stack<Node*> s;
    stack<int> sums;
    s.push(root);
    sums.push(root->data);
    while (!s.empty()) {
        Node* node = s.top(); s.pop();
        int sum = sums.top(); sums.pop();
        if (node->left == NULL && node->right == NULL) {
            if (sum == targetSum) return true;
        }
        if (node->left != NULL) {
            s.push(node->left);
            sums.push(sum + node->left->data);
        }
        if (node->right != NULL) {
            s.push(node->right);
            sums.push(sum + node->right->data);
        }
    }
    return false;
}

int main() {
    Node* root = new Node(10);
    root->left = new Node(8);
    root->right = new Node(2);
    root->left->left = new Node(3);
    root->left->right = new Node(5);
    root->right->left = new Node(2);


    int targetSum = 23;
    if (hasPathSum(root, targetSum)) {
          cout << "There is a root-to-leaf path with sum "
             << targetSum;
    }
    else {
          cout << "There is no root-to-leaf path with sum "
             << targetSum;
    }
    return 0;
}

Java

import java.util.Stack;

class Node {
    int data;
    Node left, right;

    Node(int val) {
        data = val;
        left = right = null;
    }
}

public class PathSum {
    public static boolean hasPathSum(Node root, int targetSum) {
        if (root == null)
            return false;

        Stack<Node> stack = new Stack<>();
        Stack<Integer> sums = new Stack<>();
        stack.push(root);
        sums.push(root.data);

        while (!stack.isEmpty()) {
            Node node = stack.pop();
            int sum = sums.pop();

            if (node.left == null && node.right == null) {
                if (sum == targetSum)
                    return true;
            }

            if (node.left != null) {
                stack.push(node.left);
                sums.push(sum + node.left.data);
            }
            if (node.right != null) {
                stack.push(node.right);
                sums.push(sum + node.right.data);
            }
        }

        return false;
    }

    public static void main(String[] args) {
        Node root = new Node(10);
        root.left = new Node(8);
        root.right = new Node(2);
        root.left.left = new Node(3);
        root.left.right = new Node(5);
        root.right.left = new Node(2);

        int targetSum = 23;
        if (hasPathSum(root, targetSum)) {
            System.out.println("There is a root-to-leaf path with sum " + targetSum);
        } else {
            System.out.println("There is no root-to-leaf path with sum " + targetSum);
        }
    }
}

Python3

class Node:
    def __init__(self, val):
        self.data = val
        self.left = None
        self.right = None

def hasPathSum(root, targetSum):
    if not root:
        return False
    s = [root]
    sums = [root.data]
    while s:
        node = s.pop()
        sum_val = sums.pop()
        if not node.left and not node.right:
            if sum_val == targetSum:
                return True
        if node.left:
            s.append(node.left)
            sums.append(sum_val + node.left.data)
        if node.right:
            s.append(node.right)
            sums.append(sum_val + node.right.data)
    return False

if __name__ == '__main__':
    root = Node(10)
    root.left = Node(8)
    root.right = Node(2)
    root.left.left = Node(3)
    root.left.right = Node(5)
    root.right.left = Node(2)

    targetSum = 23
    if hasPathSum(root, targetSum):
        print("There is a root-to-leaf path with sum", targetSum)
    else:
        print("There is no root-to-leaf path with sum", targetSum)

C#

using System;
using System.Collections.Generic;

public class Node
{
    public int data;
    public Node left, right;

    public Node(int val)
    {
        data = val;
        left = right = null;
    }
}

public class PathSum
{
    public static bool HasPathSum(Node root, int targetSum)
    {
        if (root == null)
            return false;

        Stack<Node> stack = new Stack<Node>();
        Stack<int> sums = new Stack<int>();
        stack.Push(root);
        sums.Push(root.data);

        while (stack.Count > 0)
        {
            Node node = stack.Pop();
            int sum = sums.Pop();

            if (node.left == null && node.right == null)
            {
                if (sum == targetSum)
                    return true;
            }

            if (node.left != null)
            {
                stack.Push(node.left);
                sums.Push(sum + node.left.data);
            }
            if (node.right != null)
            {
                stack.Push(node.right);
                sums.Push(sum + node.right.data);
            }
        }

        return false;
    }

    public static void Main(string[] args)
    {
        Node root = new Node(10);
        root.left = new Node(8);
        root.right = new Node(2);
        root.left.left = new Node(3);
        root.left.right = new Node(5);
        root.right.left = new Node(2);

        int targetSum = 23;
        if (HasPathSum(root, targetSum))
        {
            Console.WriteLine("There is a root-to-leaf path with sum " + targetSum);
        }
        else
        {
            Console.WriteLine("There is no root-to-leaf path with sum " + targetSum);
        }
    }
}

Javascript

class Node {
    constructor(val) {
        this.data = val;
        this.left = null;
        this.right = null;
    }
}

function hasPathSum(root, targetSum) {
    if (root === null) {
        return false;
    }

    const stack = [];
    const sums = [];
    stack.push(root);
    sums.push(root.data);

    while (stack.length > 0) {
        const node = stack.pop();
        const sum = sums.pop();

        if (node.left === null && node.right === null) {
            if (sum === targetSum) {
                return true;
            }
        }

        if (node.left !== null) {
            stack.push(node.left);
            sums.push(sum + node.left.data);
        }
        if (node.right !== null) {
            stack.push(node.right);
            sums.push(sum + node.right.data);
        }
    }

    return false;
}

const root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
root.right.left = new Node(2);

const targetSum = 23;
if (hasPathSum(root, targetSum)) {
    console.log("There is a root-to-leaf path with sum " + targetSum);
} else {
    console.log("There is no root-to-leaf path with sum " + targetSum);
}

Output

There is a root-to-leaf path with sum 23

Time Complexity: O(N)
Auxiliary Space: O( N)

References: http://cslibrary.stanford.edu/110/BinaryTrees.html
Author: Tushar Roy
Please write comments if you find any bug in above code/algorithm, or find other ways to solve the same problem