Remove exactly one element from the array such that max – min is minimum
Last Updated :
12 Oct, 2022
Given an array consisting of N positive integer numbers. The task is to remove exactly one element from this array to minimize max(a) – min(a) and print the minimum possible (max(a) – min(a)).
Note: max(a) means largest number in array 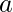 and min(a) means smallest number in array
and min(a) means smallest number in array 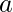 .
.
There are at least 2 elements in the array.
Examples:
Input: arr[] = {1, 3, 3, 7}
Output: 2
Remove 7, then max(a) will be 3 and min(a) will be 1.
So our answer will be 3-1 = 2.
Input: arr[] = {1, 1000}
Output: 0
Remove either 1 or 1000, then our answer will 1-1 =0 or
1000-1000=0
Simple Approach: Here it can be seen that we always have to remove either minimum or maximum of the array. We first sort the array. After sorting, if we remove minimum element, the difference would be a[n-1] – a[1]. And if we remove the maximum element, difference would be a[n-2] – a[0]. We return minimum of these two differences.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int max_min(int a[], int n)
{
sort(a, a + n);
return min(a[n - 2] - a[0], a[n - 1] - a[1]);
}
int main()
{
int a[] = { 1, 3, 3, 7 };
int n = sizeof(a) / sizeof(a[0]);
cout << max_min(a, n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int max_min(int a[], int n)
{
Arrays.sort(a);
return Math.min(a[n - 2] - a[0], a[n - 1] - a[1]);
}
public static void main(String []args)
{
int a[] = { 1, 3, 3, 7 };
int n = a.length;
System.out.println(max_min(a, n));
}
}
|
Python3
def max_min(a, n):
a.sort()
return min(a[n - 2] - a[0],
a[n - 1] - a[1])
a = [1, 3, 3, 7]
n = len(a)
print(max_min(a, n))
|
C#
using System;
class GFG
{
static int max_min(int []a, int n)
{
Array.Sort(a);
return Math.Min(a[n - 2] - a[0], a[n - 1] - a[1]);
}
public static void Main()
{
int []a = { 1, 3, 3, 7 };
int n = a.Length;
Console.WriteLine(max_min(a, n));
}
}
|
PHP
<?php
function max_min(&$a, $n)
{
sort($a);
return min($a[$n - 2] - $a[0],
$a[$n - 1] - $a[1]);
}
$a = array(1, 3, 3, 7);
$n = sizeof($a);
echo(max_min($a, $n));
?>
|
Javascript
<script>
function max_min(a, n)
{
a.sort();
return Math.min(a[n - 2] - a[0], a[n - 1] - a[1]);
}
let a = [ 1, 3, 3, 7 ];
let n = a.length;
document.write(max_min(a, n));
</script>
|
Time Complexity: O(n log n)
Auxiliary Space: O(1)
Efficient Approach:
An efficient approach is to do following.
- Find first minimum and second minimum
- Find first maximum and second maximum
- Return the minimum of following two differences.
- First maximum and second minimum
- Second maximum and first minimum
C++
#include <bits/stdc++.h>
using namespace std;
int max_min(int a[], int n)
{
if (n <= 1)
return INT_MAX;
int f_min = a[0], s_min = INT_MAX;
int f_max = a[0], s_max = INT_MIN;
for (int i = 1; i<n ;i++)
{
if (a[i] <= f_min)
{
s_min = f_min;
f_min = a[i];
}
else if (a[i] < s_min)
{
s_min = a[i];
}
if (a[i] >= f_max)
{
s_max = f_max;
f_max = a[i];
}
else if (a[i] > s_max)
{
s_max = a[i];
}
}
return min((f_max - s_min), (s_max - f_min));
}
int main()
{
int a[] = { 1, 3, 3, 7 };
int n = sizeof(a) / sizeof(a[0]);
cout << max_min(a, n);
return 0;
}
|
Java
class GFG
{
static int max_min(int a[], int n)
{
if (n <= 1)
return Integer.MAX_VALUE;
int f_min = a[0], s_min = Integer.MAX_VALUE;
int f_max = a[0], s_max = Integer.MIN_VALUE;
for (int i = 1; i<n ;i++)
{
if (a[i] <= f_min)
{
s_min = f_min;
f_min = a[i];
}
else if (a[i] < s_min)
{
s_min = a[i];
}
if (a[i] >= f_max)
{
s_max = f_max;
f_max = a[i];
}
else if (a[i] > s_max)
{
s_max = a[i];
}
}
return Math.min((f_max - s_min), (s_max - f_min));
}
public static void main(String []args)
{
int a[] = { 1, 3, 3, 7 };
int n = a.length;
System.out.println(max_min(a, n));
}
}
|
Python3
import sys
def max_min(a, n) :
if (n <= 1) :
return sys.maxsize
f_min = a[0]
s_min = sys.maxsize
f_max = a[0]
s_max = -(sys.maxsize - 1)
for i in range(n) :
if (a[i] <= f_min) :
s_min = f_min
f_min = a[i]
elif (a[i] < s_min) :
s_min = a[i]
if (a[i] >= f_max) :
s_max = f_max
f_max = a[i]
elif (a[i] > s_max) :
s_max = a[i]
return min((f_max - s_min), (s_max - f_min))
if __name__ == "__main__" :
a = [ 1, 3, 3, 7 ]
n = len(a)
print(max_min(a, n))
|
C#
using System;
class GFG
{
static int max_min(int []a, int n)
{
if (n <= 1)
return Int32.MaxValue;
int f_min = a[0], s_min = Int32.MaxValue;
int f_max = a[0], s_max = Int32.MinValue;
for (int i = 1; i<n ;i++)
{
if (a[i] <= f_min)
{
s_min = f_min;
f_min = a[i];
}
else if (a[i] < s_min)
{
s_min = a[i];
}
if (a[i] >= f_max)
{
s_max = f_max;
f_max = a[i];
}
else if (a[i] > s_max)
{
s_max = a[i];
}
}
return Math.Min((f_max - s_min), (s_max - f_min));
}
public static void Main()
{
int []a = { 1, 3, 3, 7 };
int n = a.Length;
Console.WriteLine(max_min(a, n));
}
}
|
PHP
<?php
function max_min($a, $n)
{
if ($n <= 1)
return PHP_INT_MAX;
$f_min = $a[0];
$s_min = PHP_INT_MAX;
$f_max = $a[0];
$s_max = ~PHP_INT_MAX;
for ($i = 1; $i < $n ;$i++)
{
if ($a[$i] <= $f_min)
{
$s_min = $f_min;
$f_min = $a[$i];
}
else if ($a[$i] < $s_min)
{
$s_min = $a[$i];
}
if ($a[$i] >= $f_max)
{
$s_max = $f_max;
$f_max = $a[$i];
}
else if ($a[$i] > $s_max)
{
$s_max = $a[$i];
}
}
return min(($f_max - $s_min),
($s_max - $f_min));
}
$a = array ( 1, 3, 3, 7 );
$n = sizeof($a);
echo(max_min($a, $n));
?>
|
Javascript
<script>
function max_min(a, n)
{
if (n <= 1)
return Number.MAX_VALUE;
let f_min = a[0], s_min = Number.MAX_VALUE;
let f_max = a[0], s_max = Number.MIN_VALUE;
for (let i = 1; i<n ;i++)
{
if (a[i] <= f_min)
{
s_min = f_min;
f_min = a[i];
}
else if (a[i] < s_min)
{
s_min = a[i];
}
if (a[i] >= f_max)
{
s_max = f_max;
f_max = a[i];
}
else if (a[i] > s_max)
{
s_max = a[i];
}
}
return Math.min((f_max - s_min), (s_max - f_min));
}
let a = [ 1, 3, 3, 7 ];
let n = a.length;
document.write(max_min(a, n));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...