Regular expression to ∈-NFA
Last Updated :
24 Jan, 2023
Prerequisite – Finite Automata Introduction, Designing Finite Automata from Regular Expression (Set 1)
∈-NFA is similar to the NFA but have minor difference by epsilon move. This automaton replaces the transition function with the one that allows the empty string ∈ as a possible input. The transitions without consuming an input symbol are called ∈-transitions. In the state diagrams, they are usually labeled with the Greek letter ∈. ∈-transitions provide a convenient way of modeling the systems whose current states are not precisely known: i.e., if we are modeling a system and it is not clear whether the current state (after processing some input string) should be q or q’, then we can add an ∈-transition between these two states, thus putting the automaton in both states simultaneously.
One way to implement regular expressions is to convert them into a finite automaton, known as an ∈-NFA (epsilon-NFA). An ∈-NFA is a type of automaton that allows for the use of “epsilon” transitions, which do not consume any input. This means that the automaton can move from one state to another without consuming any characters from the input string.
The process of converting a regular expression into an ∈-NFA is as follows:
- Create a single start state for the automaton, and mark it as the initial state.
- For each character in the regular expression, create a new state and add an edge between the previous state and the new state, with the character as the label.
- For each operator in the regular expression (such as “*” for zero or more, “+” for one or more, and “?” for zero or one), create new states and add the appropriate edges to represent the operator.
- Mark the final state as the accepting state, which is the state that is reached when the regular expression is fully matched.
Common regular expression used in make ∈-NFA: 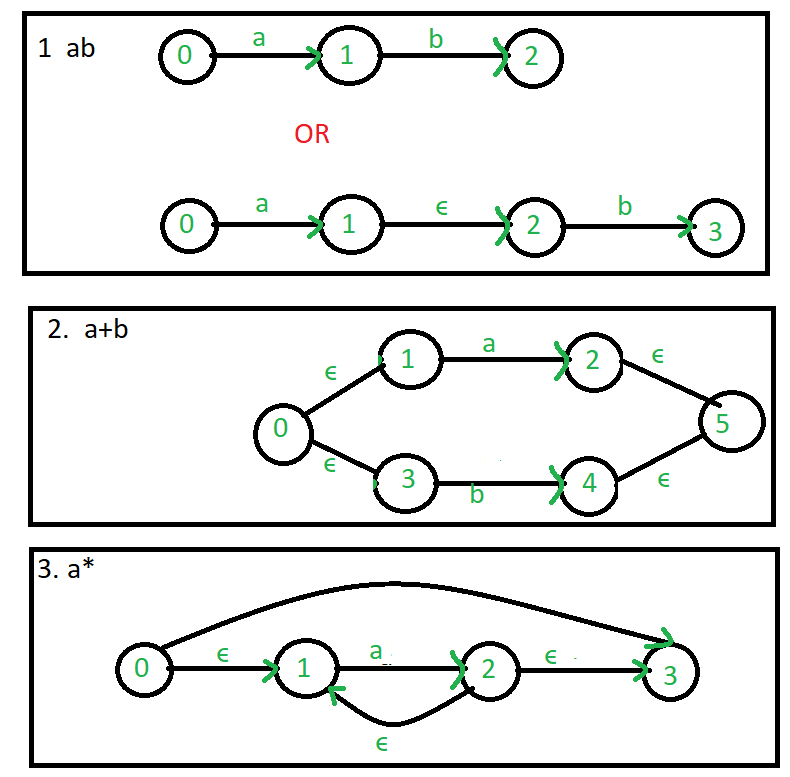 Example: Create a ∈-NFA for regular expression: (a/b)*a
Example: Create a ∈-NFA for regular expression: (a/b)*a 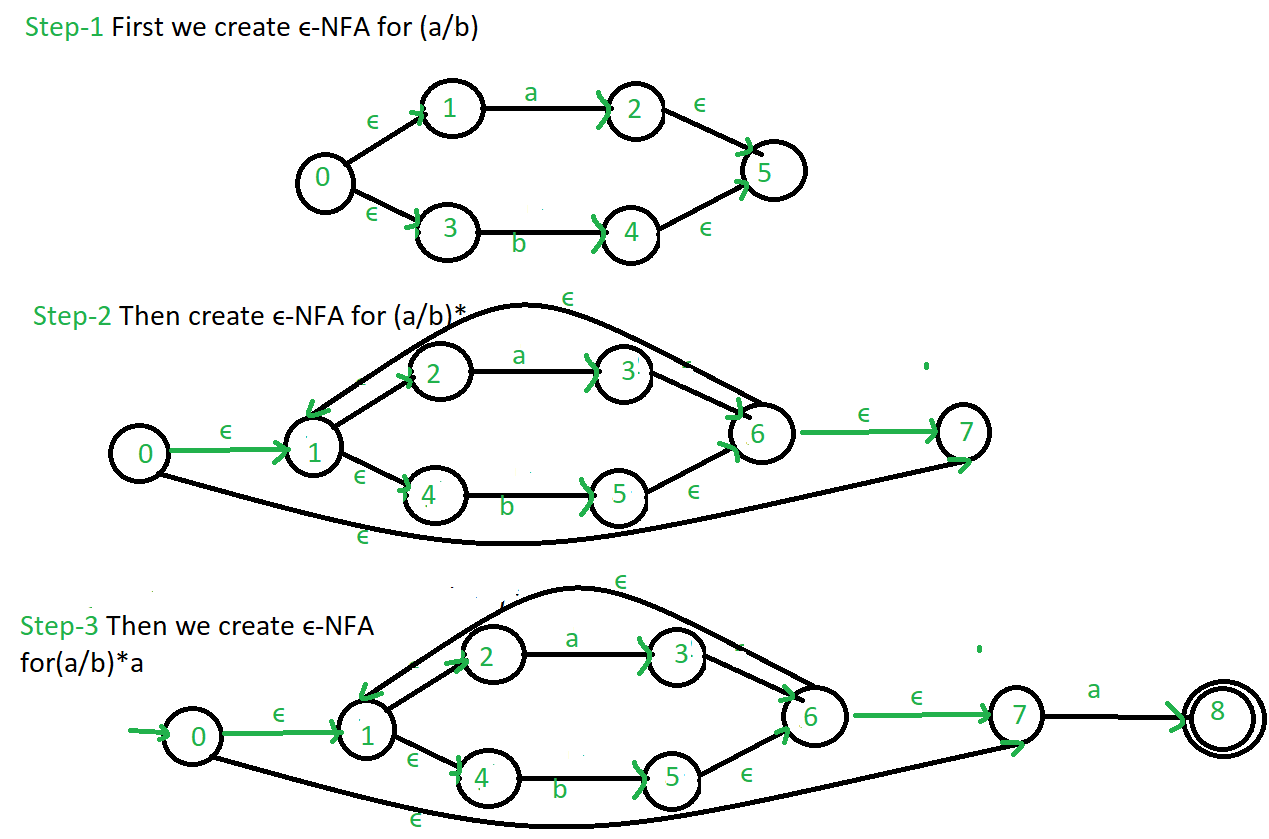 Refer for – Conversion from NFA to DFA, Minimization of DFA
Refer for – Conversion from NFA to DFA, Minimization of DFA
Share your thoughts in the comments
Please Login to comment...