DFA minimization stands for converting a given DFA to its equivalent DFA with minimum number of states. DFA minimization is also called as Optimization of DFA and uses partitioning algorithm.
Minimization of DFA
Suppose there is a DFA D < Q, Δ, q0, Δ, F > which recognizes a language L. Then the minimized DFA D < Q’, Δ, q0, Δ, F’ > can be constructed for language L as:
Step 1: We will divide Q (set of states) into two sets. One set will contain all final states and other set will contain non-final states. This partition is called P0.
Step 2: Initialize k = 1
Step 3: Find Pk by partitioning the different sets of Pk-1. In each set of Pk-1, we will take all possible pair of states. If two states of a set are distinguishable, we will split the sets into different sets in Pk.
Step 4: Stop when Pk = Pk-1 (No change in partition)
Step 5: All states of one set are merged into one. No. of states in minimized DFA will be equal to no. of sets in Pk.
How to find whether two states in partition Pk are distinguishable ?
Two states ( qi, qj ) are distinguishable in partition Pk if for any input symbol a, Δ ( qi, a ) and Δ ( qj, a ) are in different sets in partition Pk-1.
Example
Consider the following DFA shown in figure.

Step 1. P0 will have two sets of states. One set will contain q1, q2, q4 which are final states of DFA and another set will contain remaining states. So P0 = { { q1, q2, q4 }, { q0, q3, q5 } }.
Step 2. To calculate P1, we will check whether sets of partition P0 can be partitioned or not:
i) For set { q1, q2, q4 } :
Δ( q1, 0 ) = Δ ( q2, 0 ) = q2 and Δ ( q1, 1 ) = Δ( q2, 1 ) = q5, So q1 and q2 are not distinguishable.
Similarly, Δ( q1, 0 ) = Δ ( q4, 0 ) = q2 and Δ ( q1, 1 ) = Δ ( q4, 1 ) = q5, So q1 and q4 are not distinguishable.
Since, q1 and q2 are not distinguishable and q1 and q4 are also not distinguishable, So q2 and q4 are not distinguishable. So, { q1, q2, q4 } set will not be partitioned in P1.
ii) For set { q0, q3, q5 } :
Δ ( q0, 0 ) = q3 and Δ ( q3, 0 ) = q0
Δ( q0, 1) = q1 and Δ( q3, 1 ) = q4
Moves of q0 and q3 on input symbol 0 are q3 and q0 respectively which are in same set in partition P0. Similarly, Moves of q0 and q3 on input symbol 1 are q1 and q4 which are in same set in partition P0. So, q0 and q3 are not distinguishable.
Δ( q0, 0 ) = q3 and Δ( q5, 0 ) = q5 and Δ( q0, 1 ) = q1 and Δ ( q5, 1 ) = q5
Moves of q0 and q5 on input symbol 1 are q1 and q5 respectively which are in different set in partition P0. So, q0 and q5 are distinguishable. So, set { q0, q3, q5 } will be partitioned into { q0, q3 } and { q5 }. So,
P1 = { { q1, q2, q4 }, { q0, q3}, { q5 } }
To calculate P2, we will check whether sets of partition P1 can be partitioned or not:
iii)For set { q1, q2, q4 } :
Δ ( q1, 0 ) = Δ ( q2, 0 ) = q2 and Δ ( q1, 1 ) = Δ( q2, 1 ) = q5, So q1 and q2 are not distinguishable.
Similarly, Δ ( q1, 0 ) = Δ ( q4, 0 ) = q2 and Δ( q1, 1 ) = Δ( q4, 1 ) = q5, So q1 and q4 are not distinguishable.
Since, q1 and q2 are not distinguishable and q1 and q4 are also not distinguishable, So q2 and q4 are not distinguishable. So, { q1, q2, q4 } set will not be partitioned in P2.
iv)For set { q0, q3 } :
Δ ( q0, 0 ) = q3 and Δ( q3, 0 ) = q0
Δ ( q0, 1 ) = q1 and Δ ( q3, 1 ) = q4
Moves of q0 and q3 on input symbol 0 are q3 and q0 respectively which are in same set in partition P1. Similarly, Moves of q0 and q3 on input symbol 1 are q1 and q4 which are in same set in partition P1. So, q0 and q3 are not distinguishable.
v) For set { q5 }:
Since we have only one state in this set, it can’t be further partitioned. So,
P2 = { { q1, q2, q4 }, { q0, q3 }, { q5 } }
Since, P1=P2. So, this is the final partition. Partition P2 means that q1, q2 and q4 states are merged into one. Similarly, q0 and q3 are merged into one. Minimized DFA corresponding to DFA of Figure 1 is shown in Figure 2 as:
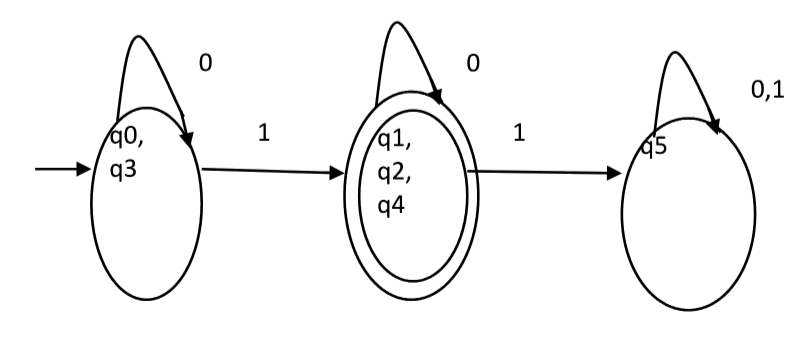
Question : Consider the given DFA. Which of the following is false?
1. Complement of L(A) is context-free.
2. L(A) = L ( ( 11 * 0 + 0 ) ( 0 + 1 )* 0* 1* )
3. For the language accepted by A, A is the minimal DFA.
4. A accepts all strings over { 0, 1 } of length atleast two.

A. 1 and 3 only
B. 2 and 4 only
C. 2 and 3 only
D. 3 and 4 only
Solution : Statement 4 says, it will accept all strings of length atleast 2. But it accepts 0 which is of length 1. So, 4 is false.
Statement 3 says that the DFA is minimal. We will check using the algorithm discussed above.
P0 = { { q2 }, { q0, q1 } }
P1 = { q2 }, { q0, q1 } }. Since, P0 = P1, P1 is the final DFA. q0 and q1 can be merged. So minimal DFA will have two states. Therefore, statement 3 is also false.
So correct option is (D).
This article has been contributed by Sonal Tuteja.
Advantages:
Reduced Complexity: Minimizing a DFA reduces its complexity by eliminating redundant states and transitions. The resulting minimized DFA is typically smaller and simpler, making it easier to understand, analyze, and modify. Minimization improves the efficiency of executing the DFA and reduces the resources required for its implementation.
Optimal Space Utilization: A minimized DFA occupies less memory and storage space compared to the original DFA. By eliminating redundant states, the minimized DFA requires fewer resources to store and represent its states and transitions. This is advantageous when working with large DFAs or limited memory environments.
Improved Performance: Minimizing a DFA can significantly improve its performance in terms of speed and efficiency. With fewer states and transitions, the minimized DFA requires fewer computations and memory accesses, resulting in faster execution. This is particularly beneficial when processing large input strings or handling real-time applications.
Language Equivalence: Minimization ensures that the resulting DFA is language equivalent to the original DFA. That is, it recognizes the same language, accepting the same valid strings and rejecting the same invalid strings. Minimization preserves the language semantics while improving the DFA’s structure.
Disadvantages:
Increased Computational Complexity: Minimizing a DFA involves performing state equivalence calculations and merging equivalent states. The computational complexity of the minimization process can be significant, especially for large DFAs. As the DFA’s size grows, the time and computational resources required for minimization increase, making it computationally expensive in some cases.
Additional Design and Analysis Effort: Minimization requires additional design and analysis effort compared to working with the original DFA. Determining state equivalence and merging equivalent states often involves careful analysis of the DFA’s structure and transition patterns. This process can be time-consuming and error-prone, requiring attention to detail.
Loss of Readability: In some cases, the minimized DFA may become less readable and intuitive compared to the original DFA. The merging of equivalent states may result in complex state representations, making it more challenging to interpret the DFA’s behavior or understand its structure.
Limited to Deterministic Automata: Minimization techniques are applicable only to deterministic automata like DFAs. Non-deterministic automata, such as NFAs, cannot be directly minimized. Converting an NFA to a DFA before minimizing it adds an additional step and may lead to an increase in the DFA’s size.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...