Register Allocation Algorithms in Compiler Design
Last Updated :
29 Dec, 2020
Register allocation is an important method in the final phase of the compiler . Registers are faster to access than cache memory . Registers are available in small size up to few hundred Kb .Thus it is necessary to use minimum number of registers for variable allocation . There are three popular Register allocation algorithms .
- Naive Register Allocation
- Linear Scan Algorithm
- Chaitin’s Algorithm
These are explained as following below.
1. Naïve Register Allocation :
- Naive (no) register allocation is based on the assumption that variables are stored in Main Memory .
- We can’t directly perform operations on variables stored in Main Memory .
- Variables are moved to registers which allows various operations to be carried out using ALU .
- ALU contains a temporary register where variables are moved before performing arithmetic and logic operations .
- Once operations are complete we need to store the result back to the main memory in this method .
- Transferring of variables to and fro from Main Memory reduces the overall speed of execution .
a = b + c
d = a
c = a + d
Variables stored in Main Memory :
| a |
b |
c |
d |
| 2 fp |
4 fp |
6 fp |
8 fp |
Machine Level Instructions :
LOAD R1, _4fp
LOAD R2, _6fp
ADD R1, R2
STORE R1, _2fp
LOAD R1, _2fp
STORE R1, _8fp
LOAD R1, _2fp
LOAD R2, _8fp
ADD R1, R2
STORE R1, _6fp
Advantages :
- Easy to understand operations and the flow of variables from Main memory to Registers and vice versa .
- Only 2 registers are enough to perform any operations .
- Design complexity is less .
Disadvantages :
- Time complexity increases as variables is moved to registers from main memory .
- Too many LOAD and STORE instructions .
- To access a variable second time we need to STORE it to the Main Memory to record any changes made and LOAD it again .
- This method is not suitable for modern compilers .
2. Linear Scan Algorithm :
- Linear Scan Algorithm is a global register allocation mechanism .
- It is a bottom up approach .
- If n variables are live at any point of time then we require ‘n’ registers .
- In this algorithm the variables are scanned linearly to determine the live ranges of the variable based on which the registers are allocated .
- The main idea behind this algorithm is that to allocate minimum number of registers such that these registers can be used again and this totally depends upon the live range of the variables .
- For this algorithm we need to implement live variable analysis of Code Optimization .
a = b + c
d = e + f
d = d + e
IFZ a goto L0
b = a + d
goto L1
L0 : b = a - d
L1 : i = b
Control Flow Graph :
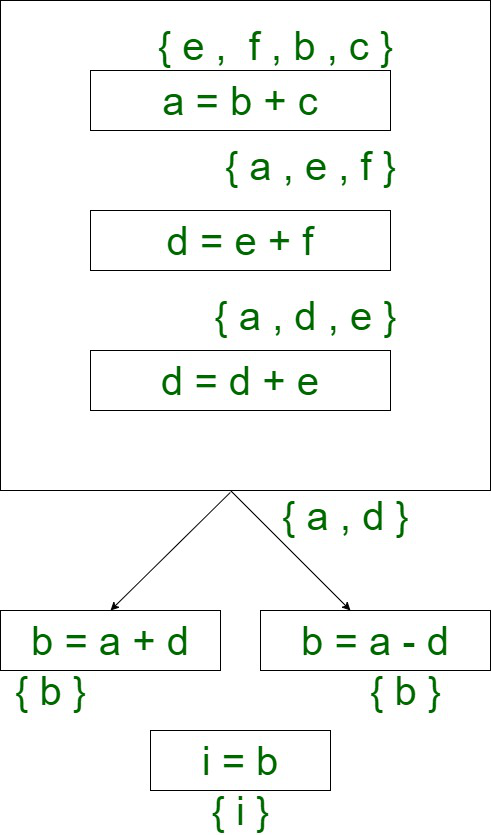
- At any point of time the maximum number of live variables is 4 in this example . Thus we require 4 registers at maximum for register allocation .
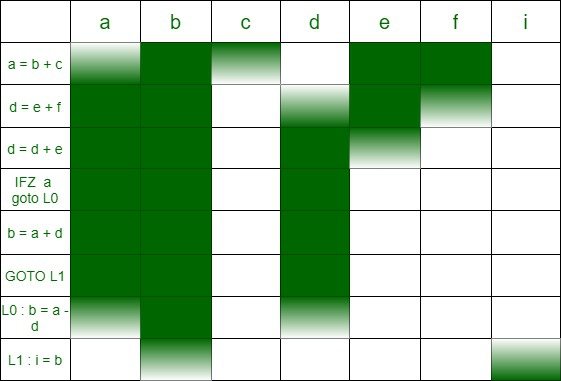
If we draw horizontal line at any point on the above diagram we can see that we require exactly 4 registers to perform the operations in the program .
Splitting :
- Sometimes the required number of registers may not be available . In such case we may require to move some variables to and from the RAM . This is known as spilling .
- Spilling can be done effectively by moving the variable which is used less number of times in the program .
Disadvantages :
- Linear Scan Algorithm doesn’t take into account the “lifetime holes” of the variable .
- Variables are not live throughout the program and this algorithm fails to record the holes in the live range of the variable .
3.Graph Coloring (Chaitin’s Algorithm) :
- Register allocation is interpreted as a graph coloring problem .
- Nodes represent live range of the variable.
- Edges represent the connection between two live ranges .
- Assigning color to the nodes such that no two adjacent nodes have same color .
- Number of colors represents the minimum number of registers required .
A k-coloring of the graph is mapped to k registers .
Steps :
- Choose an arbitrary node of degree less than k .
- Push that node onto the stack and remove all of it’s outgoing edges .
- Check if the remaining edges have degree less than k, if YES goto 5 else goto #
- If the degree of any remaining vertex is less than k then push it onto to the stack .
- If there is no more edge available to push and if all edges are present in the stack POP each node and color them such that no two adjacent nodes have same color.
- Number of colors assigned to nodes is the minimum number of registers needed .
# spill some nodes based on their live ranges and then try again with same k value . If problem persists it means that the assumed k value can’t be the minimum number of registers .Try increasing the k value by 1 and try the whole procedure again .
For the same instructions mentioned above the graph coloring will be as follows :
Assuming k=4

before coloring
After performing the graph coloring, final graph is obtained as follows

final graph with k(4) colors
Note : Any color(register) can be assigned to ‘i’ as it has no edge to any other nodes .
Share your thoughts in the comments
Please Login to comment...