Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands.
Below is an iterative algorithm for insertion sort
Algorithm
// Sort an arr[] of size n
insertionSort(arr, n)
Loop from i = 1 to n-1.
a) Pick element arr[i] and insert
it into sorted sequence arr[0..i-1] Example:
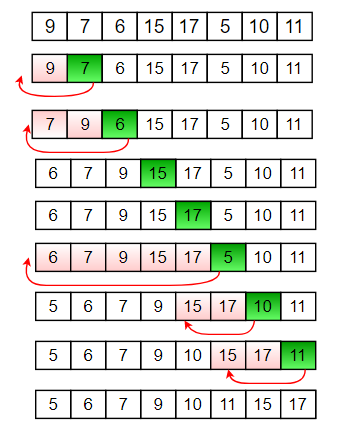
Refer Insertion Sort for more details.
How to implement it recursively?
Recursive Insertion Sort has no performance/implementation advantages, but can be a good question to check one’s understanding of Insertion Sort and recursion.
If we take a closer look at Insertion Sort algorithm, we keep processed elements sorted and insert new elements one by one in the sorted array.
Recursion Idea.
- Base Case: If array size is 1 or smaller, return.
- Recursively sort first n-1 elements.
- Insert last element at its correct position in sorted array.
Below is implementation of above idea.
C++
#include <iostream>
using namespace std;
void insertionSortRecursive(int arr[], int n)
{
if (n <= 1)
return;
insertionSortRecursive( arr, n-1 );
int last = arr[n-1];
int j = n-2;
while (j >= 0 && arr[j] > last)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = last;
}
void printArray(int arr[], int n)
{
for (int i=0; i < n; i++)
cout << arr[i] <<" ";
}
int main()
{
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr)/sizeof(arr[0]);
insertionSortRecursive(arr, n);
printArray(arr, n);
return 0;
}
|
C
#include <stdio.h>
void insertionSortRecursive(int arr[], int n)
{
if (n <= 1)
return;
insertionSortRecursive(arr, n - 1);
int last = arr[n - 1];
int j = n - 2;
while (j >= 0 && arr[j] > last) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = last;
}
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSortRecursive(arr, n);
printArray(arr, n);
return 0;
}
|
Java
import java.util.Arrays;
public class GFG
{
static void insertionSortRecursive(int arr[], int n)
{
if (n <= 1)
return;
insertionSortRecursive( arr, n-1 );
int last = arr[n-1];
int j = n-2;
while (j >= 0 && arr[j] > last)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = last;
}
public static void main(String[] args)
{
int arr[] = {12, 11, 13, 5, 6};
insertionSortRecursive(arr, arr.length);
System.out.println(Arrays.toString(arr));
}
}
|
Python3
def insertionSortRecursive(arr,n):
if n<=1:
return
insertionSortRecursive(arr,n-1)
last = arr[n-1]
j = n-2
while (j>=0 and arr[j]>last):
arr[j+1] = arr[j]
j = j-1
arr[j+1]=last
def printArray(arr,n):
for i in range(n):
print(arr[i],end=" ")
arr = [12,11,13,5,6]
n = len(arr)
insertionSortRecursive(arr, n)
printArray(arr, n)
|
C#
using System;
class GFG
{
static void insertionSortRecursive(int []arr,
int n)
{
if (n <= 1)
return;
insertionSortRecursive(arr, n - 1);
int last = arr[n - 1];
int j = n - 2;
while (j >= 0 && arr[j] > last)
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = last;
}
static void Main()
{
int []arr = {12, 11, 13, 5, 6};
insertionSortRecursive(arr, arr.Length);
for(int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}
}
|
PHP
<?php
function insertionSortRecursive(&$arr, $n)
{
if ($n <= 1)
return;
insertionSortRecursive($arr, $n - 1);
$last = $arr[$n - 1];
$j = $n - 2;
while ($j >= 0 && $arr[$j] > $last)
{
$arr[$j + 1] = $arr[$j];
$j--;
}
$arr[$j + 1] = $last;
}
function printArray(&$arr, $n)
{
for ($i = 0; $i < $n; $i++)
echo $arr[$i]." ";
}
$arr = array(12, 11, 13, 5, 6);
$n = sizeof($arr);
insertionSortRecursive($arr, $n);
printArray($arr, $n);
?>
|
Javascript
<script>
function insertionSortRecursive(arr,n)
{
if (n <= 1)
return;
insertionSortRecursive( arr, n-1 );
let last = arr[n-1];
let j = n-2;
while (j >= 0 && arr[j] > last)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = last;
}
let arr=[12, 11, 13, 5, 6];
insertionSortRecursive(arr, arr.length);
for(let i=0;i<arr.length;i++)
{
document.write(arr[i]+" ");
}
</script>
|
Output :
5 6 11 12 13
Time Complexity: O(n2)
Auxiliary Space: O(n)
https://www.youtube.com/watch?v=wObxd4Kx8sE
This article is contributed by Sahil Chhabra. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.about the topic discussed above