Rectangular (or Pronic) Numbers
Last Updated :
15 Sep, 2023
The numbers that can be arranged to form a rectangle are called Rectangular Numbers (also known as Pronic numbers). The first few rectangular numbers are:
0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 . . . . . .
Given a number n, find n-th rectangular number.
Examples:
Input : 1
Output : 2
Input : 4
Output : 20
Input : 5
Output : 30
The number 2 is a rectangular number because it is 1 row by 2 columns. The number 6 is a rectangular number because it is 2 rows by 3 columns, and the number 12 is a rectangular number because it is 3 rows by 4 columns.
If we observe these numbers carefully, we can notice that n-th rectangular number is n(n+1).
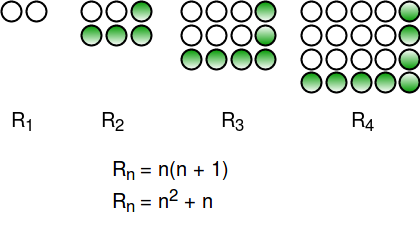
C++
#include <bits/stdc++.h>
using namespace std;
int findRectNum(int n)
{
return n * (n + 1);
}
int main()
{
int n = 6;
cout << findRectNum(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int findRectNum(int n)
{
return n * (n + 1);
}
public static void main(String[] args)
{
int n = 6;
System.out.println(findRectNum(n));
}
}
|
C#
using System;
class GFG {
static int findRectNum(int n)
{
return n * (n + 1);
}
public static void Main()
{
int n = 6;
Console.Write(findRectNum(n));
}
}
|
Python
def findRectNum(n):
return n*(n + 1)
n = 6
print (findRectNum(n))
|
PHP
<?php
function findRectNum($n)
{
return $n * ($n + 1);
}
$n = 6;
echo findRectNum($n);
?>
|
Javascript
<script>
function findRectNum(n)
{
return n * (n + 1);
}
var n = 6;
document.write(findRectNum(n));
</script>
|
Output:
42
Time complexity: O(1) since performing constant operations
Space complexity: O(1) since using constant space for variables
Check if a given number is Pronic | Efficient Approach
Share your thoughts in the comments
Please Login to comment...