Rectangular (or Pronic) Numbers

The numbers that can be arranged to form a rectangle are called Rectangular Numbers (also known as Pronic numbers). The first few rectangular numbers are: 
0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 . . . . . . 
Given a number n, find n-th rectangular number.
Examples: 

Input : 1
Output : 2

Input : 4
Output : 20

Input : 5
Output : 30

The number 2 is a rectangular number because it is 1 row by 2 columns. The number 6 is a rectangular number because it is 2 rows by 3 columns, and the number 12 is a rectangular number because it is 3 rows by 4 columns. 
If we observe these numbers carefully, we can notice that n-th rectangular number is n(n+1).

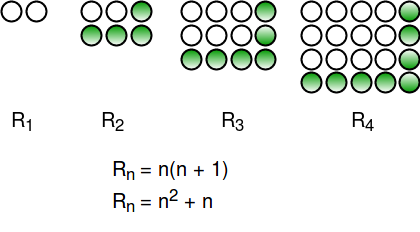
C++

// CPP Program to find n-th rectangular number
#include <bits/stdc++.h>
using namespace std;

// Returns n-th rectangular number
int findRectNum(int n)
{
    return n * (n + 1);
}

// Driver code
int main()
{
    int n = 6;
    cout << findRectNum(n);
    return 0;
}

Java

// Java Program to find n-th rectangular number
import java.io.*;

class GFG {

    // Returns n-th rectangular number
    static int findRectNum(int n)
    {
        return n * (n + 1);
    }

    // Driver code
    public static void main(String[] args)
    {
        int n = 6;
        System.out.println(findRectNum(n));
    }
}

// This code is contributed by vt_m.

C#

// C# Program to find n-th rectangular number

using System;

class GFG {

    // Returns n-th rectangular number
    static int findRectNum(int n)
    {
        return n * (n + 1);
    }

    // Driver code
    public static void Main()
    {
        int n = 6;
        Console.Write(findRectNum(n));
    }
}

// This code is contributed by vt_m.

Python

# Python3 Program to find n-th rectangular number

# Returns n-th rectangular number
def findRectNum(n):
    return n*(n + 1)

# Driver code
n = 6
print (findRectNum(n))

# This code is contributed by Shreyanshi Arun.

PHP

<?php
// PHP Program to find n-th
// rectangular number

// Returns n-th rectangular
// number
function findRectNum($n)
{
    return $n * ($n + 1);
}

    // Driver Code
    $n = 6;
    echo findRectNum($n);

// This code is contributed by ajit
?>

Javascript

<script>

// Javascript Program to find n-th rectangular number

// Returns n-th rectangular number
function findRectNum(n)
{
    return n * (n + 1);
}

// Driver code
var n = 6;
document.write(findRectNum(n));

// This code is contributed by noob2000.
</script>

Output: 

42

Time complexity: O(1) since performing constant operations

Space complexity: O(1) since using constant space for variables

Check if a given number is Pronic | Efficient Approach
This article is contributed by DANISH_RAZA . If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.