Python | sympy.binomial() method
Last Updated :
07 Jul, 2019
With the help of
sympy.binomial() method, we can find the number of ways to choose
k items from a set of
n distinct items. It is also often written as
nCk, and is pronounced “n choose k”.
(1) 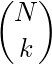
Syntax: binomial(N, K)
Parameters:
N – It denotes the number of items to choose from.
K – It denotes the number of items to choose.
Returns: Returns the number of ways to choose K items from a set of N distinct items
Example #1:
from sympy import *
N = 4
K = 2
print("N = {}, K = {}".format(N, K))
comb = binomial(N, K)
print("N choose K : {}".format(comb))
|
Output:
N = 4, K = 2
N choose K : 6
Example #2:
from sympy import *
N, K = symbols('A B')
print("N = {}, K = {}".format(N, K))
comb = binomial(N, K)
print("N choose K : {}".format(comb))
|
Output:
N = A, K = B
N choose K : binomial(A, B)
Share your thoughts in the comments
Please Login to comment...