Python | Plotting Fibonacci spiral fractal using Turtle
Last Updated :
14 May, 2021
What is Fractal Geometry?
Fractal geometry is a special form of graphical representation of mathematical functions or set of numbers generated by a mathematical function. It is a recursive, detailed and infinitely self-similar set of mathematics. These geometrical representations exhibit “Unfolding Symmetry”. Unfolding symmetry is the property of geometrical structures to retain a self-similar pattern at infinitesimally small scale.
We know Fibonacci Series follows a recursive relation f(n) = f(n-1) + f(n-2), where n is the nth term in the series. Again f(0) = 0, f(1) = 1
Approach of plotting Fibonacci Fractal
Each number in the series represent the length of the sides of a square. The square of side length 0 does not exist. So we start from square of side length 1. The next square is also of side length 1.
- We first construct the two squares of dimension 1 side by side as shown in the image below.
- Then taking the joint length of the two squares we construct a third square below the two squares of dimension 1. Now the square is of the dimension 2
- Again taking the 2 squares of dimension 1, 2 respectively we construct the fourth square of dimension 3
- Although we continued this process for a small number of iterations but this process continues till infinity.
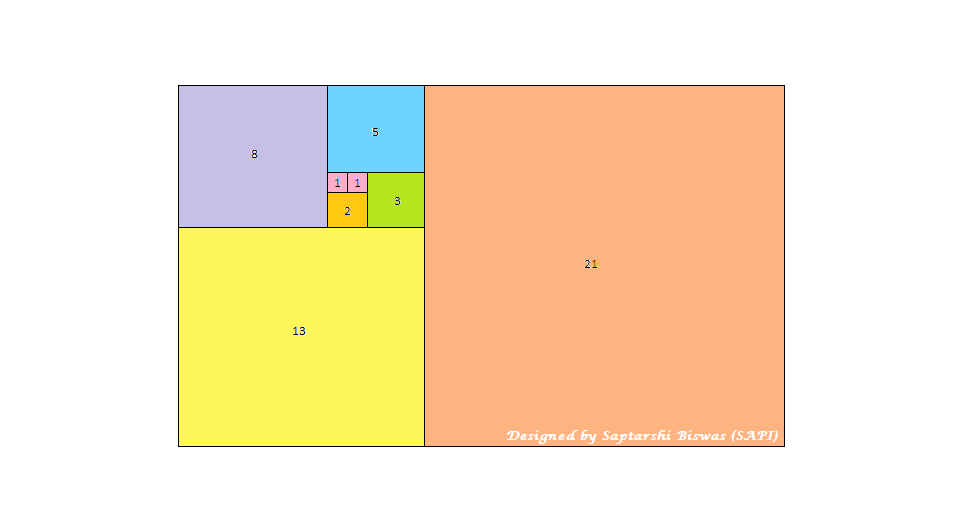
After we complete drawing the squares we start with the innermost smallest square. Then we draw continuous quadrants within the squares with the side of each square as the radius.
Below is the implementation:
Python3
import turtle
import math
def fiboPlot(n):
a = 0
b = 1
square_a = a
square_b = b
x.pencolor("blue")
x.forward(b * factor)
x.left(90)
x.forward(b * factor)
x.left(90)
x.forward(b * factor)
x.left(90)
x.forward(b * factor)
temp = square_b
square_b = square_b + square_a
square_a = temp
for i in range(1, n):
x.backward(square_a * factor)
x.right(90)
x.forward(square_b * factor)
x.left(90)
x.forward(square_b * factor)
x.left(90)
x.forward(square_b * factor)
temp = square_b
square_b = square_b + square_a
square_a = temp
x.penup()
x.setposition(factor, 0)
x.seth(0)
x.pendown()
x.pencolor("red")
x.left(90)
for i in range(n):
print(b)
fdwd = math.pi * b * factor / 2
fdwd /= 90
for j in range(90):
x.forward(fdwd)
x.left(1)
temp = a
a = b
b = temp + b
factor = 1
n = int(input('Enter the number of iterations (must be > 1): '))
if n > 0:
print("Fibonacci series for", n, "elements :")
x = turtle.Turtle()
x.speed(100)
fiboPlot(n)
turtle.done()
else:
print("Number of iterations must be > 0")
|
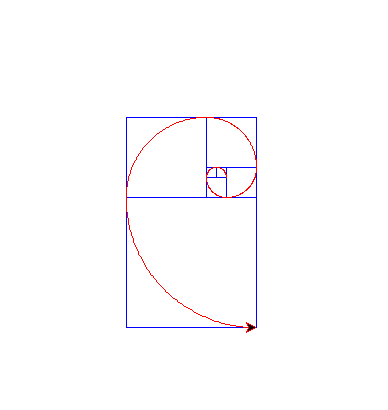
Output:
Share your thoughts in the comments
Please Login to comment...