A Pythagorean triplet whose two numbers are 8 and 10, then what is the third number?
Last Updated :
01 Apr, 2024
The third number of the Pythagorean triplet is 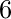 .
.
A Pythagoras Theorem is defined for the Right-angled triangles. Pythagoras theorem defines relationships among the sides of the right-angled triangle. The theorem is also known as the Pythagorean theorem and is defined as “The square of the hypotenuse is equal to the sum of the squares of the other two sides, perpendicular, and the base.” The perpendicular and base of the right-angled triangle are the two sides that are at 90° to each other and the hypotenuse is known as the third side.
Pythagoras Formula
The formula is defined with the help of the theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides of a right angles triangle,

(Hypotenuse)2 = Perpendicular2 + Base2
H2 = P2 + B2
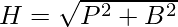
Now, lets move to the question, as it is given that that two numbers are 8 and 10, you must be wondering why as the values of two sides are given, but it is not given that if the sides are hypotenuse, perpendicular or base.
Let’s say that the triplets are required to be written as  is the unknown triplet.
is the unknown triplet.
Since,  is the largest number given in the question and hypotenuse is the largest side, lets assume that hypotenuse is
is the largest number given in the question and hypotenuse is the largest side, lets assume that hypotenuse is 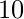 units and perpendicular is
units and perpendicular is 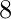 units.
units.
According to the formula for Pythagoras theorem,
H2 = P2 +B2
⇒ 102 = 82 + x2
⇒ 100 = 64 + x2
⇒ x2 = 100 – 64
⇒ x2 = 36
⇒ x = √36
⇒ x = 6 units.
So, the triplets are  and the third number for the Pythagorean triplet is
and the third number for the Pythagorean triplet is 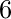 .
.
Share your thoughts in the comments
Please Login to comment...