Proof that Collinearity Problem is NP Complete
Last Updated :
02 Nov, 2023
Problem: Given 3 points a, b, c, the task is to check if these three points are collinear.
Explanation: An instance of the problem is an input specified to the problem. An instance of the collinearity problem is three points ((ax, ay), (bx, by), (cx, cy)). Since an NP-Complete is a problem which is both in NP and NP-hard, the proof for the statement that a problem is NP-Complete consists of two parts:
- The problem itself is in NP class.
- All other problems in NP class can be polynomial-time reducible to that.
(B is polynomial-time reducible to C is denoted as B ≤ PC)
If the 2nd condition is only satisfied then the problem is called NP-Hard.
But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. That is why to show a problem is NP-complete, prove that the problem is in NP and any NP-Complete problem is reducible to that. Thus, it can be verified that the collinearity problem is NP-Complete using the following propositions:
Collinearity Problem is in NP:
If any problem is in NP, then given a ‘certificate’, which is a solution to the problem and an instance of the problem (a collection of three points a, b, c) we will be able to identify(whether the solution is correct or not) certificate in polynomial time. This can be done by checking:
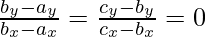
Collinearity problem is NP-Hard:
In order to prove the Collinearity problem is NP-Hard, deduce a reduction from a known NP-Hard problem, that is, 3-Sum to collinearity problem. For each x in the 3-Sum instance, map from x to (x, x3). Now, from 3 Sum instances (x, y, z) we have ((x, x3), (y, y3), (z, z3)).
The following propositions hold:
Let set S has collinear points (x, x3), (y, y3), (z, z3)
Now,
=> 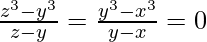 =>
=> 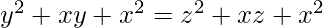 =>
=> 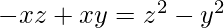 =>
=> 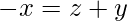 =>
=> 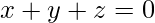
Therefore, (x, y, z) are collinear points. These equations are interchangeable.
Therefore, the Collinearity Problem is NP-Complete.
Share your thoughts in the comments
Please Login to comment...