Proof that Hamiltonian Cycle is NP-Complete
Last Updated :
16 Dec, 2022
Prerequisite: NP-Completeness, Hamiltonian cycle.
Hamiltonian Cycle:
A cycle in an undirected graph G=(V, E) traverses every vertex exactly once.
Problem Statement: Given a graph G=(V, E), the problem is to determine if graph G contains a Hamiltonian cycle consisting of all the vertices belonging to V.
Explanation: An instance of the problem is an input specified to the problem. An instance of the Independent Set problem is a graph G=(V, E), and the problem is to check whether the graph can have a Hamiltonian Cycle in G. Since an NP-Complete problem, by definition, is a problem which is both in NP and NP-hard, the proof for the statement that a problem is NP-Complete consists of two parts:
- The problem itself is in NP class.
- All other problems in NP class can be polynomial-time reducible to that. (B is polynomial-time reducible to C is denoted as
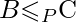 )
)
If the 2nd condition is only satisfied then the problem is called NP-Hard. But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. That is why if we want to show a problem is NP-Complete, we just show that the problem is in NP and if any NP-Complete problem is reducible to that, then we are done, i.e. if B is NP-Complete and 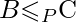 for C in NP, then C is NP-Complete.
for C in NP, then C is NP-Complete.
- Hamiltonian Cycle is in NP If any problem is in NP, then, given a ‘certificate’, which is a solution to the problem and an instance of the problem (a graph G and a positive integer k, in this case), we will be able to verify (check whether the solution given is correct or not) the certificate in polynomial time. The certificate is a sequence of vertices forming Hamiltonian Cycle in the graph. We can validate this solution by verifying that all the vertices belong to the graph and each pair of vertices belonging to the solution are adjacent. This can be done in polynomial time, that is O(V +E) using the following strategy for graph G(V, E):
flag=true
For every pair {u, v} in the subset V’:
Check that these two have an edge between them
If there is no edge, set flag to false and break
If flag is true:
Solution is correct
Else:
Solution is incorrect- Hamiltonian Cycle is NP Hard In order to prove the Hamiltonian Cycle is NP-Hard, we will have to reduce a known NP-Hard problem to this problem. We will carry out a reduction from the Hamiltonian Path problem to the Hamiltonian Cycle problem. Every instance of the Hamiltonian Path problem consisting of a graph G =(V, E) as the input can be converted to Hamiltonian Cycle problem consisting of graph G’ = (V’, E’). We will construct the graph G’ in the following way:
- V’ = Add vertices V of the original graph G and add an additional vertex Vnew such that all the vertices connected of the graph are connected to this vertex. The number of vertices increases by 1, V’ =V+1.
- E’ = Add edges E of the original graph G and add new edges between the newly added vertex and the original vertices of the graph. The number of edges increases by the number of vertices V, that is, E’=E+V.
- Let us assume that the graph G contains a hamiltonian path covering the V vertices of the graph starting at a random vertex say Vstart and ending at Vend, now since we connected all the vertices to an arbitrary new vertex Vnew in G’. We extend the original Hamiltonian Path to a Hamiltonian Cycle by using the edges Vend to Vnew and Vnew to Vstart respectively. The graph G’ now contains the closed cycle traversing all vertices once.
- We assume that the graph G’ has a Hamiltonian Cycle passing through all the vertices, inclusive of Vnew. Now to convert it to a Hamiltonian Path, we remove the edges corresponding to the vertex Vnew in the cycle. The resultant path will cover the vertices V of the graph and will cover them exactly once.
 Thus we can say that the graph G’ contains a Hamiltonian Cycle if graph G contains a Hamiltonian Path. Therefore, any instance of the Hamiltonian Cycle problem can be reduced to an instance of the Hamiltonian Path problem. Thus, the Hamiltonian Cycle is NP-Hard. Conclusion: Since, the Hamiltonian Cycle is both, a NP-Problem and NP-Hard. Therefore, it is a NP-Complete problem.
Thus we can say that the graph G’ contains a Hamiltonian Cycle if graph G contains a Hamiltonian Path. Therefore, any instance of the Hamiltonian Cycle problem can be reduced to an instance of the Hamiltonian Path problem. Thus, the Hamiltonian Cycle is NP-Hard. Conclusion: Since, the Hamiltonian Cycle is both, a NP-Problem and NP-Hard. Therefore, it is a NP-Complete problem.
Share your thoughts in the comments
Please Login to comment...