Set partition is NP complete

Set partition problem: Set partition problem partitions an array of numbers into two subsets such that the sum of each of these two subsets is the same. Let S be a set of numbers and A is a subset of numbers with sum S1, then there exists another subset containing the remainder of the elements (S – A) with sum S2, and S1 is equaled to S2.  

Problem Statement: Given a set S of N numbers, the task is to determine if the set contains two partitions of S, with both of them having exactly the same sum.  

Explanation:
An instance of the problem is an input specified to the problem. An instance of the Set Partition problem is a set S, and the task is to check whether there exist any two non-overlapping partitions of S having a sum of elements as sum. Since an NP-Complete problem is a problem which is both in NP and NP-hard, the proof for the statement that a problem is NP-Complete consists of two parts:

1. The problem itself is in NP class.
2. All other problems in NP class can be polynomial-time reducible to that. (B is polynomial-time reducible to C is denoted as B ≤ P^C)

If the 2nd condition is only satisfied then the problem is called NP-Hard.

But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. Therefore, to show a problem is NP-Complete then prove that the problem is in NP and any NP-Complete problem is reducible to that i.e., if B is NP-Complete and B ≤ P^C For C in NP, then C is NP-Complete. Thus, it can be concluded that the Set partition problem is NP-Complete using the following two propositions:

Set Partition Problem is in NP:
If any problem is in NP, then, given a ‘certificate’, which is a solution to the problem and an instance of the problem (a set S and two partitions A and A’, in this case), it can be proved that the certificate in polynomial time. This can be done in the following way:  

1. For every element x in A and x’ in A’, verify that all the elements belonging to S are covered.
2. Let S1 is 0, S2 is 0
3. For every element x in A add that value to S1.
4. For every element x’ in A’ add that value to S2.
5. Verify that S1 is the same as S2.

The algorithm takes linear time in the size of the set of numbers.

Set Partition Problem is NP-Hard:
In order to prove that the Independent Set problem is NP-Hard, perform a reduction from a known NP-Hard problem to this problem. Carry out a reduction from which the Subset Sum Problem can be reduced to the Set Partition problem. The Subset Problem provides the input as a set of numbers S and a target sum t, the problem aims at finding the subset T belonging to S with a sum same as the t. Let s be the sum of members of S. Now, feed S’ = S ∪ {s − 2t} into the Set Partition problem.

Now prove that the problem of computing the set partition indeed boils down to the computation of the subset-sum. The reduction can be proved by the following two propositions:

Now, let us consider a set of the numbers T with summation equivalent to t(Subset Sum), then the remainder of the elements in S(assuming O) will have the sum o = s – t. Let us assume the original set is equal to T’ = T ∪ (s – 2t) which has a sum equal to t’. 
Now the following observations hold:

o     = s – t 
o – t = s – 2t, Difference in sum between O and T.
t’     = t + (s – 2t)
       = s – t
       = o, the sum of T’ and O are equal.

Hence, the original set can be partitioned into two subsets of sum (s – t) each. Therefore, the set partition problem is satisfied. 
Now suppose an equal-sum partitioning (A, A’) of S’ = S ∪ {s − 2t} exists. The sum of each partition is given by:

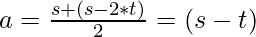
Consider the partition containing the element {s – 2t} to be A’. Let A = A’- {s – 2t}. The sum of elements in A is given by:

A = s – t – {s – 2t}
   = t

Also, S’ – S = {s – 2t}. So A is a subset of S with a sum equal to t. 

Therefore, the subset sum problem is satisfied.

My Personal Notes arrow_drop_up

Save