Subset Sum is NP Complete

Prerequisite: NP-Completeness, Subset Sum Problem

Subset Sum Problem: Given N non-negative integers a₁…a_N and a target sum K, the task is to decide if there is a subset having a sum equal to K.

Explanation: An instance of the problem is an input specified to the problem. An instance of the subset sum problem is a set S = {a₁, …, a_N} and an integer K. Since an NP-complete problem is a problem which is both in NP and NP-hard, the proof for the statement that a problem is NP-Complete consists of two parts:

1. The problem itself is in NP class.
2. All other problems in NP class can be polynomial-time reducible to that. (B is polynomial-time reducible to C is denoted as B ≤ P^C)

If the 2nd condition is only satisfied then the problem is called NP-Hard.

But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. That is why if we want to show a problem is NP-Complete we just show that the problem is in NP and any NP-Complete problem is reducible to that then we are done i.e. if B is NP-Complete and B≤P^C for C in NP, then C is NP-Complete. Thus, we can verify that the Subset Sum Problem is NP-Complete using the following two propositions:

Subset Sum is in NP:
If any problem is in NP, then given a certificate, which is a solution to the problem and an instance of the problem (a set S of integer a₁…a_N and an integer K) we will be able to identify (whether the solution is correct or not) certificate in polynomial time. This can be done by checking that the sum of the integers in subset S’ is equal to K.

Subset Sum is NP-Hard:
In order to prove Subset Sum is NP-Hard, perform a reduction from a known NP-Hard problem to this problem.
Carry out a reduction from which the Vertex Cover Problem can be reduced to the Subset Sum problem. Let us assume a graph G(V, E) where V = {1, 2, …, N}. Now, for every vertex i, a_i=i. For every edge (i, j) we define a component called, b_ij.
We will represent the integers in a matrix format, where every row is expressed in the base-4 representation of the corresponding integer value of |E|+1 digits.
The matrix has the following properties:

1. The first column contains an integer value 1 for a_i and 0 for b_ij.
2. Each of the E columns starting from the right side of the matrix represents a digit for each edge. The column (i, j)=1 for a_i, a_j and b_ij, otherwise, it is equal to 0.
3. We define a constant k’ such that,

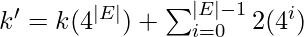
Now, the following propositions hold:

• Let us consider a subset of vertices and edges to (V’, E’) respectively, such that

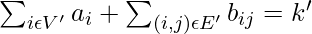
• b_ij can contain at most 1 in every column. Also, the k’ parameter has a 2 in all less significant digits up to |E|. We can never have a carry-in these digits. Now, these digits sum up to at-most three 1’s in each column. This implies that for every edge (i, j), V’ must contain either i or j. Therefore, V’ becomes a vertex cover.
• Let us assume there is a Vertex Cover of size k, we will choose integers a_i such that i lies in V’ and all b_ij Such that either i or j is in V’. On summation of all these integers in base 4 representation(that we choose from the matrix), we get sum of integers =k’. Therefore, the chosen integers form the subset of integers with sum = k’. Therefore, subset sum holds.

Let us consider the following example,  
Given is a vertex cover V = {1, 3} and k = 2 

Now, a₁ = 1, a₂ = 2, a₃ = 3, a₄ = 4

The matrix can be constructed in the following way:

=> => => 

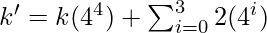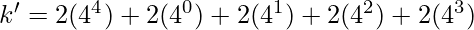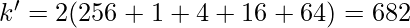
Now, to prove the value of k’ let us choose a_i such that i lies in V’, we choose a₁ and a₃ and b_ij such that either i or j lies in V’, that is we choose b_ij such that either i or j is in V’, that is we choose b₁₂, b₁₄, b₂₃ and b₃₄ from the matrix . In base 4 representation, we have the following values:

a₁ = 321, a₃ = 276, b₁₂ = 64, b₂₃ = 16, b₁₄ = 1, b₃₄ = 4

These values are computed using the matrix. On summation of these values, we get,

k’ = 321 + 276 + 64 + 16 + 1 + 4 = 682.

Hence, k’ value can be calculated and verified.

Therefore, the Subset Sum Problem is NP-Complete.