Progression – Aptitude Questions and Answers
Last Updated :
05 Sep, 2023
Progression (or Sequences and Series) are mathematical concepts that involve arranging numbers in a particular order based on a repeatable pattern. The topic of Progressions is frequently asked in various competitive exams like SSC, Bank PO, and other government job exams and is a crucial part of Quantitative Aptitude, but it can be mastered with the right formulas and working through some examples.
Practice Quiz:
Practice Progression Aptitude Quiz Questions
Arithmetic Progression (AP)
A sequence of numbers is called an arithmetic progression if the difference between any two consecutive terms is always the same. In simple terms, it means that the next number in the series is calculated by adding a fixed number to the previous number in the series. This fixed number is called the common difference. For example, 2,4,6,8,10 is an AP because the difference between any two consecutive terms in the series (common difference) is the same (4 – 2 = 6 – 4 = 8 – 6 = 10 – 8 = 2).
- nth term of an AP = a + (n-1) d
- Arithmetic Mean = Sum of all terms in the AP / Number of terms in the AP
- Sum of ‘n’ terms of an AP = 0.5 n (first term + last term) = 0.5 n [ 2a + (n-1) d ]
Geometric Progression (GP)
A sequence of numbers is called a geometric progression if the ratio of any two consecutive terms is always the same. In simple terms, it means that the next number in the series is calculated by multiplying a fixed number by the previous number in the series. This fixed number is called the common ratio. For example, 2,4,8,16 is a GP because the ratio of any two consecutive terms in the series (common difference) is the same (4 / 2 = 8 / 4 = 16 / 8 = 2).
- nth term of a GP = a rn-1
- Geometric Mean = nth root of product of n terms in the GP
- Sum of ‘n’ terms of a GP (r < 1) = [a (1 – rn)] / [1 – r]
- Sum of ‘n’ terms of a GP (r > 1) = [a (rn – 1)] / [r – 1]
- Sum of infinite terms of a GP (r < 1) = (a) / (1 – r)
Harmonic Progression (HP)
A sequence of numbers is called a harmonic progression if the reciprocal of the terms are in AP. In simple terms, a,b,c,d,e,f are in HP if 1/a, 1/b, 1/c, 1/d, 1/e, 1/f are in AP.
- Harmonic Mean = (2 a b) / (a + b)
For two numbers, if A, G, and H are respectively the arithmetic, geometric and harmonic means, then
- A ≥ G ≥ H
- A H = G2, i.e., A, G, H are in GP
Sample Questions on Progression
Q1: Find the nth term for the AP: 11, 17, 23, 29, …
Solution:
Here, a = 11, d = 17 – 11 = 23 – 17 = 29 – 23 = 6We know that nth term of an AP is a + (n – 1) d=> nth term for the given AP = 11 + (n – 1) 6=> nth term for the given AP = 5 + 6 nWe can verify the answer by putting values of ‘n’.=> n = 1 -> First term = 5 + 6 = 11=> n = 2 -> Second term = 5 + 12 = 17=> n = 3 -> Third term = 5 + 18 = 23and so on …
Q2: Find the sum of the AP in the above question till the first 10 terms.
Solution :
From the above question, => nth term for the given AP = 5 + 6 n=> First term = 5 + 6 = 11=> Tenth term = 5 + 60 = 65=> Sum of 10 terms of the AP = 0.5 n (first term + last term) = 0.5 x 10 (11 + 65)=> Sum of 10 terms of the AP = 5 x 76 = 380
Q3: For elements 4 and 6, verify that A ≥ G ≥ H.
Solution :
A = Arithmetic Mean = (4 + 6) / 2 = 5G = Geometric Mean = 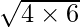 = 4.8989H = Harmonic Mean = (2 x 4 x 6) / (4 + 6) = 48 / 10 = 4.8Therefore, A ≥ G ≥ H
= 4.8989H = Harmonic Mean = (2 x 4 x 6) / (4 + 6) = 48 / 10 = 4.8Therefore, A ≥ G ≥ H
Q4: Find the sum of the series 32, 16, 8, 4, … upto infinity.
Solution :
First term, a = 32Common ratio, r = 16 / 32 = 8 / 16 = 4 / 8 = 1 / 2 = 0.5We know that for an infinite GP, Sum of terms = a / (1 – r)=> Sum of terms of the GP = 32 / (1 – 0.5) = 32 / 0.5 = 64
Q5: The sum of three numbers in a GP is 26 and their product is 216. ind the numbers.
Solution:
Let the numbers be a/r, a, ar.=> (a / r) + a + a r = 26=> a (1 + r + r2) / r = 26Also, it is given that product = 216=> (a / r) x (a) x (a r) = 216=> a3 = 216=> a = 6=> 6 (1 + r + r2) / r = 26=> (1 + r + r2) / r = 26 / 6 = 13 / 3=> 3 + 3 r + 3 r2 = 13 r=> 3 r2 – 10 r + 3 = 0=> (r – 3) (r – (1 / 3) ) = 0=> r = 3 or r = 1 / 3Thus, the required numbers are 2, 6 and 18.
Related Resources:
Problems on Progressions (AP,GP, HP) | Set-2
Test your knowledge of Progressions in Quantitative Aptitude with the quiz linked below, containing numerous practice questions to help you master the topic:-
<<Practice Progression Aptitude Questions>>
Also Practice:
Share your thoughts in the comments
Please Login to comment...