Program to find sum of the given sequence
Last Updated :
01 Mar, 2023
Given two numbers 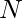 and . The task is to find the sum of the sequence given below.
and . The task is to find the sum of the sequence given below.
(1*2*3*…*k) + (2*3*…*k*(k+1)) + (3*4*..*(k+1)*(k+2)) +…..+((n-k+1)*(n-k+2)*…*(n-k+k)).
Since the output can be large, print the answer under modulo 10^9+7.
Examples:
Input : N = 3, K = 2
Output : 8
Input : N = 4, K = 2
Output : 20
Let us take the given example and try to reduce it to a general formula.
In the given example for n = 3 and k=2,
Sum = 1*2 + 2*3
We know that:
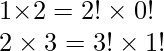
So each term is of the form:
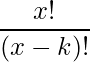
If we multiply and divide by
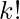
, it becomes
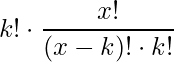
Which is nothing but,

Therefore,
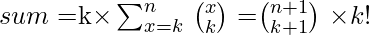
But since n is so large we can not calculate it directly, we have to simplify the above expression.
On Simplifying we get,
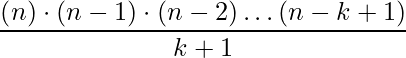
Algorithm:
- Create a static long variable named MOD and initialize it to 1000000007.
- Create a static function modInv of long return type which takes a long value as input and returns modulo inverse of x under MOD
- Create a new long variable n and set it to MOD -2
- Initialize another long variable result to 1
- start a while loop with condition n is greater than 0.
- If the least significant bit of n is 1, then multiply the result with x modulo MOD and store it in the result.
- Modulus x is squared and stored in x.
- Now shift n right by 1.
- return the final value.
- create a static function getSum with a long return type which takes two long values as input n and k
- create a long variable ans and initialize it to 1
- start a for loop from i = n + 1 to i greater than n-k and decrement i after every iteration and for each iteration Add(n + 1 – i) modulo MOD to ans and store the result.
- Modulo MOD, multiply ans by modInv(k + 1), and store the result in and.
- return ans
Below is the implementation of the above idea:
C++
#include <bits/stdc++.h>
using namespace std;
const long long MOD = 1000000007;
long long modInv(long long x)
{
long long n = MOD - 2;
long long result = 1;
while (n) {
if (n & 1)
result = result * x % MOD;
x = x * x % MOD;
n = n / 2;
}
return result;
}
long long getSum(long long n, long long k)
{
long long ans = 1;
for (long long i = n + 1; i > n - k; i--)
ans = ans * i % MOD;
ans = ans * modInv(k + 1) % MOD;
return ans;
}
int main()
{
long long n = 3, k = 2;
cout<<getSum(n,k);
return 0;
}
|
Java
class GFG {
static long MOD = 1000000007;
static long modInv(long x) {
long n = MOD - 2;
long result = 1;
while (n > 0) {
if ((n & 1) > 0) {
result = result * x % MOD;
}
x = x * x % MOD;
n = n / 2;
}
return result;
}
static long getSum(long n, long k) {
long ans = 1;
for (long i = n + 1; i > n - k; i--) {
ans = ans * i % MOD;
}
ans = ans * modInv(k + 1) % MOD;
return ans;
}
public static void main(String[] args) {
long n = 3, k = 2;
System.out.println(getSum(n, k));
}
}
|
Python3
MOD = 1000000007;
def modInv(x):
n = MOD - 2;
result = 1;
while (n):
if (n&1):
result = result * x % MOD;
x = x * x % MOD;
n = int(n / 2);
return result;
def getSum(n, k):
ans = 1;
for i in range(n + 1, n - k, -1):
ans = ans * i % MOD;
ans = ans * modInv(k + 1) % MOD;
return ans;
n = 3;
k = 2;
print(getSum(n,k));
|
C#
using System;
class gfg
{
public long MOD = 1000000007;
public long modInv(long x)
{
long n = MOD - 2;
long result = 1;
while (n >0) {
if ((n & 1) > 0)
result = result * x % MOD;
x = x * x % MOD;
n = n / 2;
}
return result;
}
public long getSum(long n, long k)
{
long ans = 1;
for (long i = n + 1; i > n - k; i--)
ans = ans * i % MOD;
ans = ans * modInv(k + 1) % MOD;
return ans;
}
}
class geek
{
public static int Main()
{
gfg g = new gfg();
long n = 3, k = 2;
Console.WriteLine(g.getSum(n,k));
return 0;
}
}
|
PHP
<?php
function modInv($x)
{
$MOD = 1000000007;
$n = $MOD - 2;
$result = 1;
while ($n)
{
if ($n & 1)
$result = $result * $x % $MOD;
$x = $x * $x % $MOD;
$n = $n / 2;
}
return $result;
}
function getSum($n, $k)
{
$MOD = 1000000007;
$ans = 1;
for ($i = $n + 1; $i > $n - $k; $i--)
$ans = $ans * $i % $MOD;
$ans = $ans * modInv($k + 1) % $MOD;
return $ans;
}
$n = 3; $k = 2;
echo getSum($n, $k);
?>
|
Javascript
<script>
var MOD = 100000007;
function modInv(x)
{
var n = MOD - 2;
var result = 1;
while (n) {
if (n & 1)
result = result * x % MOD;
x = x * x % MOD;
n = n / 2;
}
return result;
}
function getSum(n, k)
{
var ans = 1;
for (var i = n + 1; i > n - k; i--)
ans = ans * i % MOD;
ans = ans * modInv(k + 1) % MOD;
return ans;
}
var n = 3, k = 2;
document.write( getSum(n,k));
</script>
|
Time Complexity: O(k+log(m)) where k is the given number and m is the value of the modulo.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...