Program to find sum of 1 + x/2! + x^2/3! +…+x^n/(n+1)!

Given a number x and n, the task is to find the sum of the below series of x till n terms:  

Examples:

Input: x = 5, n = 2
Output: 7.67
Explanation:
    Sum of first two termed
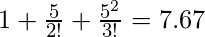    Input: x = 5, n = 4Output: 18.08Explanation: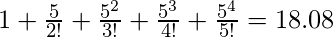 

Approach: Iterate the loop till the nth term, compute the formula in each iteration i.e.  

nth term of the series =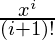 

Below is the implementation of the above approach: 

C++

// C++ Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!

#include <iostream>
#include <math.h>
using namespace std;

// Method to find the factorial of a number
int fact(int n)
{
    if (n == 1)
        return 1;

    return n * fact(n - 1);
}

// Method to compute the sum
double sum(int x, int n)
{
    double i, total = 1.0;

    // Iterate the loop till n
    // and compute the formula
    for (i = 1; i <= n; i++) {
        total = total + (pow(x, i) / fact(i + 1));
    }

    return total;
}

// Driver code
int main()
{

    // Get x and n
    int x = 5, n = 4;

    // Print output
    cout << "Sum is: " << sum(x, n);

    return 0;
}

Java

// Java Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!

public class SumOfSeries {

    // Method to find factorial of a number
    static int fact(int n)
    {
        if (n == 1)
            return 1;

        return n * fact(n - 1);
    }

    // Method to compute the sum
    static double sum(int x, int n)
    {
        double total = 1.0;

        // Iterate the loop till n
        // and compute the formula
        for (int i = 1; i <= n; i++) {
            total = total + (Math.pow(x, i) / fact(i + 1));
        }

        return total;
    }

    // Driver Code
    public static void main(String[] args)
    {

        // Get x and n
        int x = 5, n = 4;

        // Find and print the sum
        System.out.print("Sum is: " + sum(x, n));
    }
}

Python3

# Python3 Program to compute sum of
# 1 + x / 2 ! + x ^ 2 / 3 ! +...+x ^ n/(n + 1)!

# Method to find the factorial of a number
def fact(n):
    if n == 1:
        return 1
    else:
        return n * fact(n - 1)

# Method to compute the sum
def sum(x, n):
    total = 1.0

    # Iterate the loop till n
    # and compute the formula
    for i in range (1, n + 1, 1):
        total = total + (pow(x, i) / fact(i + 1))

    return total

# Driver code
if __name__== '__main__':

    # Get x and n
    x = 5
    n = 4

    # Print output
    print ("Sum is: {0:.4f}".format(sum(x, n)))

# This code is contributed by
# SURENDRA_GANGWAR

C#

// C# Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!
using System;

class SumOfSeries {

    // Method to find factorial of a number
    static int fact(int n)
    {
        if (n == 1)
            return 1;

        return n * fact(n - 1);
    }

    // Method to compute the sum
    static double sum(int x, int n)
    {
        double total = 1.0;

        // Iterate the loop till n
        // and compute the formula
        for (int i = 1; i <= n; i++) {
            total = total + (Math.Pow(x, i) / fact(i + 1));
        }

        return total;
    }

    // Driver Code
    public static void Main()
    {

        // Get x and n
        int x = 5, n = 4;

        // Find and print the sum
        Console.WriteLine("Sum is: " + sum(x, n));
    }
}

// This code is contributed
// by anuj_67..

PHP

<?php
// PHP Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!

// Function to find the factorial
// of a number
function fact($n)
{
    if ($n == 1)
        return 1;

    return $n * fact($n - 1);
}

// Function to compute the sum
function sum($x, $n)
{
    $total = 1.0;

    // Iterate the loop till n
    // and compute the formula
    for ($i = 1; $i <= $n; $i++)
    {
        $total = $total + (pow($x, $i) /
                          fact($i + 1));
    }

    return $total;
}

// Driver code

// Get x and n
$x = 5;
$n = 4;

// Print output
echo "Sum is: ", sum($x, $n);

// This code is contributed by ANKITRAI1
?>

Javascript

<script>
// java script  Program to compute sum of
// 1 + x/2! + x^2/3! +...+x^n/(n+1)!

// Function to find the factorial
// of a number
function fact(n)
{
    if (n == 1)
        return 1;

    return n * fact(n - 1);
}

// Function to compute the sum
function sum(x, n)
{
    let total = 1.0;

    // Iterate the loop till n
    // and compute the formula
    for (let i = 1; i <= n; i++)
    {
        total = total + (Math.pow(x, i) /
                        fact(i + 1));
    }

    return total.toFixed(4);
}

// Driver code

// Get x and n
let x = 5;
let n = 4;

// Print output
document.write( "Sum is: "+ sum(x, n));

// This code is contributed by sravan kumar Gottumukkala
</script>

Output:

Sum is: 18.0833

Time Complexity: O(n²)

Auxiliary Space: O(n), since n extra space has been taken.

Efficient approach: Time complexity for above algorithm is O() because for each sum iteration factorial is being calculated which is O(n). It can be observed that term of the series can be written as , where . Now we can iterate over to calculate the sum.
Below is the implementation of the above approach:

C++

// C++ implementation of the approach
#include <iostream>
using namespace std;

// Function to compute the series sum
double sum(int x, int n)
{
    double total = 1.0;

    // To store the value of S[i-1]
    double previous = 1.0;

    // Iterate over n to store sum in total
    for (int i = 1; i <= n; i++)
    {

        // Update previous with S[i]
        previous = (previous * x) / (i + 1);
        total = total + previous;
    }
    return total;
}

// Driver code
int main()
{
    // Get x and n
    int x = 5, n = 4;

    // Find and print the sum
    cout << "Sum is: " << sum(x, n);

    return 0;
}

// This code is contributed by jit_t

Java

// Java implementation of the approach

public class GFG {

    // Function to compute the series sum
    static double sum(int x, int n)
    {

        double total = 1.0;

        // To store the value of S[i-1]
        double previous = 1.0;

        // Iterate over n to store sum in total
        for (int i = 1; i <= n; i++) {

            // Update previous with S[i]
            previous = (previous * x) / (i + 1);
            total = total + previous;
        }

        return total;
    }

    // Driver code
    public static void main(String[] args)
    {

        // Get x and n
        int x = 5, n = 4;

        // Find and print the sum
        System.out.print("Sum is: " + sum(x, n));
    }
}

Python3

# Python implementation of the approach

# Function to compute the series sum
def sum(x, n):
    total = 1.0;

    # To store the value of S[i-1]
    previous = 1.0;

    # Iterate over n to store sum in total
    for i in range(1, n + 1):

        # Update previous with S[i]
        previous = (previous * x) / (i + 1);
        total = total + previous;

    return total;

# Driver code
if __name__ == '__main__':

    # Get x and n
    x = 5;
    n = 4;

    # Find and print the sum
    print("Sum is: ", sum(x, n));

# This code is contributed by 29AjayKumar

C#

// C# implementation of the approach
using System;

class GFG
{

    // Function to compute the series sum
    public double sum(int x, int n)
    {
        double total = 1.0;

        // To store the value of S[i-1]
        double previous = 1.0;

        // Iterate over n to store sum in total
        for (int i = 1; i <= n; i++)
        {

            // Update previous with S[i]
            previous = ((previous * x) / (i + 1));
            total = total + previous;
        }

        return total;
    }
}

// Driver code
class geek
{
    public static void Main()
    {
        GFG g = new GFG();

        // Get x and n
        int x = 5, n = 4;

        // Find and print the sum
        Console.WriteLine("Sum is: " + g.sum(x, n));
    }
}

// This code is contributed by SoM15242

Javascript

<script>
    // Javascript implementation of the approach

    // Function to compute the series sum
    function sum(x, n)
    {
        let total = 1.0;

        // To store the value of S[i-1]
        let previous = 1.0;

        // Iterate over n to store sum in total
        for (let i = 1; i <= n; i++)
        {

            // Update previous with S[i]
            previous = ((previous * x) / (i + 1));
            total = total + previous;
        }

        return total;
    }

    // Get x and n
    let x = 5, n = 4;

    // Find and print the sum
    document.write("Sum is: " + sum(x, n));

</script>

Output:

Sum is: 18.083333333333336

Time Complexity: O(n)
Auxiliary Space: O(1) since using constant variables