Program to find if two numbers and their AM and HM are present in an array using STL
Last Updated :
22 Sep, 2022
Given an array of Number and two values A and B, The task is to check the following Conditions:
- If two numbers are present in the array or not.
- If Yes, then their Arithmetic Mean and Harmonic Mean are also present in the same array or not.
- If all conditions are satisfied, Print the Geometric Mean of the two numbers.
The respective means of the numbers can be formulated as follows:
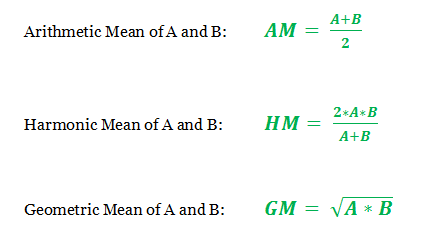
Examples:
Input: arr[] = {1.0, 2.0, 2.5, 3.0, 4.0, 4.5, 5.0, 6.0}, A = 3, B = 6.
Output : GM = 4.24
Explanation:
A = 3, B = 6 are present in the array.
AM = 4.5, HM = 4 are also present in the array.
So, GM = 4.24
Input: arr = {1.0, 2.0, 2.5, 3.0, 4.0, 4.5, 5.0, 6.0}, A = 4, B = 6.
Output: AM and HM not found
Approach:
- The idea is to use Hashing, using which we can simply store the array elements in a Hash container and use constant time O(1) operations to find and track the numbers and their means. Finally, the Geometric Mean is computed if all the conditions are satisfied by observing the simple relation AM * HM = GM2.
- A step-wise implementation of the above approach is as follows:
- A Hash container is defined to store the array elements.
- The arithmetic and harmonic means are calculated based on the formulae.
- Simple conditional statements are used to find the elements in the Hash container in constant time.
- Provided, all conditions are satisfied, the GM is calculated from above relation.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float ArithmeticMean(float A, float B)
{
return (A + B) / 2;
}
float HarmonicMean(float A, float B)
{
return (2 * A * B) / (A + B);
}
void CheckArithmeticHarmonic(float arr[],
float A,
float B, int N)
{
float AM = ArithmeticMean(A, B);
float HM = HarmonicMean(A, B);
unordered_set<float> Hash;
for (int i = 0; i < N; i++)
{
Hash.insert(arr[i]);
}
if (Hash.find(A) != Hash.end()
&& Hash.find(B) != Hash.end()) {
if (Hash.find(AM) != Hash.end()
&& Hash.find(HM) != Hash.end()) {
cout << "GM = ";
printf("%0.2f", sqrt(AM * HM));
}
else
{
cout << "AM and HM not found";
}
}
else
{
cout << "Numbers not found";
}
}
int main()
{
float arr[] = {1.0, 2.0, 2.5, 3.0, 4.0,
4.5, 5.0, 6.0};
int N = sizeof(arr)/sizeof(arr[0]);
float A = 3.0;
float B = 6.0;
CheckArithmeticHarmonic(arr, A, B, N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static Double ArithmeticMean(Double A, Double B)
{
return (A + B) / 2;
}
static Double HarmonicMean(Double A, Double B)
{
return (2 * A * B) / (A + B);
}
static void CheckArithmeticHarmonic(Double arr[],
Double A,
Double B, int N)
{
Double AM = ArithmeticMean(A, B);
Double HM = HarmonicMean(A, B);
HashMap<Double,
Integer> Hash = new HashMap<Double,
Integer>();
for(int i = 0; i < N; i++)
{
Hash.put(arr[i], 1);
}
if (Hash.get(A) != 0 &&
Hash.get(B) != 0)
{
if (Hash.get(AM) != 0 &&
Hash.get(HM) != 0)
{
System.out.print("GM = ");
System.out.format("%.2f", Math.sqrt(AM * HM));
}
else
{
System.out.print("AM and HM not found");
}
}
else
{
System.out.print("numbers not found");
}
}
public static void main(String args[])
{
Double arr[] = { 1.0, 2.0, 2.5, 3.0,
4.0, 4.5, 5.0, 6.0};
int N = (arr.length);
Double A = 3.0;
Double B = 6.0;
CheckArithmeticHarmonic(arr, A, B, N);
}
}
|
Python3
from math import sqrt
def ArithmeticMean(A, B):
return (A + B) / 2
def HarmonicMean(A, B):
return (2 * A * B) / (A + B)
def CheckArithmeticHarmonic(arr, A, B, N):
AM = ArithmeticMean(A, B)
HM = HarmonicMean(A, B)
Hash = set()
for i in range(N):
Hash.add(arr[i])
if (A in Hash and B in Hash):
if (AM in Hash and HM in Hash):
print("GM =", round(sqrt(AM * HM), 2))
else:
print("AM and HM not found")
else:
print("Numbers not found")
if __name__ == '__main__':
arr = [ 1.0, 2.0, 2.5, 3.0,
4.0, 4.5, 5.0, 6.0 ]
N = len(arr)
A = 3.0
B = 6.0
CheckArithmeticHarmonic(arr, A, B, N)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static Double ArithmeticMean(Double A, Double B)
{
return (A + B) / 2;
}
static Double HarmonicMean(Double A, Double B)
{
return (2 * A * B) / (A + B);
}
static void CheckArithmeticHarmonic(Double []arr,
Double A,
Double B, int N)
{
Double AM = ArithmeticMean(A, B);
Double HM = HarmonicMean(A, B);
Dictionary<Double,
int> Hash = new Dictionary<Double,
int>();
for(int i = 0; i < N; i++)
{
Hash[arr[i]] = 1;
}
if (Hash.ContainsKey(A) &&
Hash.ContainsKey(B))
{
if (Hash.ContainsKey(AM) &&
Hash.ContainsKey(HM))
{
Console.Write("GM = ");
Console.Write(Math.Round(
Math.Sqrt(AM * HM), 2));
}
else
{
Console.WriteLine("AM and HM not found");
}
}
else
{
Console.WriteLine("numbers not found");
}
}
public static void Main()
{
Double []arr = { 1.0, 2.0, 2.5, 3.0,
4.0, 4.5, 5.0, 6.0 };
int N = (arr.Length);
Double A = 3.0;
Double B = 6.0;
CheckArithmeticHarmonic(arr, A, B, N);
}
}
|
Javascript
<script>
function ArithmeticMean(A, B)
{
return ((A + B) / 2);
}
function HarmonicMean(A, B)
{
return (2 * A * B) / (A + B);
}
function CheckArithmeticHarmonic(arr, A, B, N)
{
let AM = ArithmeticMean(A, B);
let HM = HarmonicMean(A, B);
let Hash = new Map();
for(let i = 0; i < N; i++)
{
Hash.set(arr[i], 1);
}
if (Hash.get(A) != 0 &&
Hash.get(B) != 0)
{
if (Hash.get(AM) != 0 &&
Hash.get(HM) != 0)
{
document.write("GM = ");
document.write(Math.sqrt(AM * HM).toFixed(2));
}
else
{
document.write("AM and HM not found");
}
}
else
{
document.write("numbers not found");
}
}
let arr = [ 1.0, 2.0, 2.5, 3.0,
4.0, 4.5, 5.0, 6.0];
let N = (arr.length);
let A = 3.0;
let B = 6.0;
CheckArithmeticHarmonic(arr, A, B, N);
</script>
|
Complexity Analysis:
The overall time complexity of the above program is based on the initial iteration of the array elements at user-defined input. The find operations associated with the Set are all O(1) constant-time operations. Therefore,
Time complexity: of the program is O(N) where N is the size of the array.
Auxiliary space: O(N) because it is using extra space for unordered_set
Share your thoughts in the comments
Please Login to comment...