Program for Stirling Interpolation Formula
Last Updated :
14 Nov, 2022
Given n number of floating values x, and their corresponding functional values f(x), estimate the value of the mathematical function for any intermediate value of the independent variable x, i.e., at x = a.
Examples:
Input : n = 5
x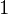 = 0, x
= 0, x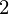 = 0.5, x
= 0.5, x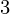 = 1.0, x
= 1.0, x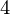 = 1.5, x
= 1.5, x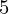 = 2.0 f(x
= 2.0 f(x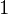 ) = 0, f(x
) = 0, f(x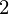 ) = 0.191, f(x
) = 0.191, f(x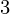 ) = 0.341, f(x
) = 0.341, f(x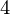 ) = 0.433, f(x
) = 0.433, f(x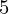 ) = 0.477 a = 1.22Output : The value of function at 1.22 is 0.389 .As can be seen f(1.0) = 0.341 and f(1.5) = 0.433, so f(1.22) should be somewhere in between these two values . Using Stirling Approximation, f(1.22)comes out to be 0.389.Input : n = 7 x
) = 0.477 a = 1.22Output : The value of function at 1.22 is 0.389 .As can be seen f(1.0) = 0.341 and f(1.5) = 0.433, so f(1.22) should be somewhere in between these two values . Using Stirling Approximation, f(1.22)comes out to be 0.389.Input : n = 7 x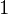 = 0, x
= 0, x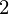 = 5, x
= 5, x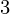 = 10, x
= 10, x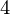 = 15, x
= 15, x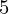 = 20, x
= 20, x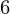 = 25, x
= 25, x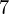 = 30 f(x
= 30 f(x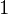 ) = 0, f(x
) = 0, f(x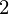 ) = 0.0875, f(x
) = 0.0875, f(x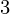 ) = 0.1763, f(x
) = 0.1763, f(x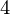 ) = 0.2679, f(x
) = 0.2679, f(x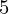 ) = 0.364, f(x
) = 0.364, f(x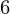 ) = 0.4663, f(x
) = 0.4663, f(x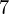 ) = 0.5774 a = 16Output : The value of function at 16 is 0.2866 .
) = 0.5774 a = 16Output : The value of function at 16 is 0.2866 .
Stirling Interpolation
Stirling Approximation or Stirling Interpolation Formula is an interpolation technique, which is used to obtain the value of a function at an intermediate point within the range of a discrete set of known data points .
Stirling Formula is obtained by taking the average or mean of the Gauss Forward and Gauss Backward Formula . Both the Gauss Forward and Backward formula are formulas for obtaining the value of the function near the middle of the tabulated set .
How to find
Stirling Approximation involves the use of a forward difference table, which can be prepared from the given set of x and f(x) or y as given below –

This table is prepared with the help of x and its corresponding f(x) or y . Then, each of the next column values is computed by calculating the difference between its preceding and succeeding values in the previous column, like 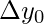 = y
= y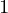 – y
– y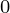 ,
, 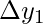 = y
= y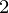 – y
– y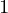 ,
, 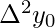 =
= 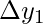 –
– 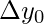 , and so on.
, and so on.
Now, the Gauss Forward Formula for obtaining f(x) or y at a is:
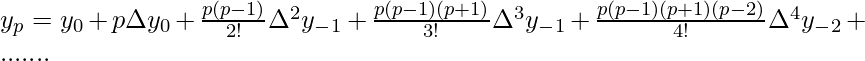
where,
p = 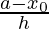 ,
,
a is the point where we have to determine f(x), x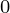 is the selected value from the given x which is closer to a (generally, a value from the middle of the table is selected), and h is the difference between any two consecutive x. Now, y
is the selected value from the given x which is closer to a (generally, a value from the middle of the table is selected), and h is the difference between any two consecutive x. Now, y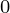 becomes the value corresponding to x
becomes the value corresponding to x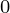 and values before x
and values before x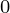 have negative subscript and those after
have negative subscript and those after 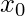 have positive subscript, as shown in the table below –
have positive subscript, as shown in the table below –

And the Gauss Backward Formula for obtaining f(x) or y at a is :
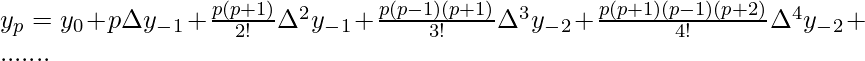
Now, taking the mean of the above two formulas and obtaining the formula for Stirling Approximation as given below –
![Rendered by QuickLaTeX.com P_2_n(x) = y_0 + q.\frac{\Delta y_-_1+\Delta y_0}{2}+\frac{q^2}{2!},\Delta^2 y_-_1 +\frac{q(q^2-1)}{3!}.\frac{\Delta^3 y_-_2 + \Delta^3 y_-_1}{2}+\frac{q^2(q^2-1)}{4!}. \Delta ^4 y_-_2 + \frac{q(q^2-1)(q^2-2^2)}{5!}.\frac{\Delta ^5 y_-_3+ \Delta ^5y_-_2}{2}+\frac{q^2(q^2-1)(q^2-2^2)}{6!}.\Delta^6y_-_3+....+ \frac{q(q^2-1)(q^2-2^2)(q^2-3^2)...[q^2-(n-1)^2]}{(2n-1)!}* \frac{\Delta ^{2n-1}y_-_n+ \Delta ^{2n-1}y_-_{n-1}}{2}+\frac{q^2(q^2-1)(q^2-2^2)...[q^2-(n-1)^2]}{(2n)!} \Delta^{2n}y_{-n},](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9955be1c936bc151d4e0fa27fcdc715c_l3.png)
Here, q is the same as p in Gauss formulas, and the rest of the symbols are the same.
When To Use
- Stirling Approximation is useful when q lies between
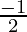 and
and 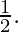
- Outside this range, it can still be used, but the accuracy of the computed value would be less.
- It gives the best estimate for the range
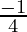 < q <
< q < 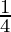 .
.
C++
#include <bits/stdc++.h>
using namespace std;
void Stirling(float x[], float fx[], float x1,
int n)
{
float h, a, u, y1 = 0, N1 = 1, d = 1,
N2 = 1, d2 = 1, temp1 = 1, temp2 = 1,
k = 1, l = 1, delta[n][n];
int i, j, s;
h = x[1] - x[0];
s = floor(n / 2);
a = x[s];
u = (x1 - a) / h;
for (i = 0; i < n - 1; ++i) {
delta[i][0] = fx[i + 1] - fx[i];
}
for (i = 1; i < n - 1; ++i) {
for (j = 0; j < n - i - 1; ++j) {
delta[j][i] = delta[j + 1][i - 1]
- delta[j][i - 1];
}
}
y1 = fx[s];
for (i = 1; i <= n - 1; ++i) {
if (i % 2 != 0) {
if (k != 2) {
temp1 *= (pow(u, k) -
pow((k - 1), 2));
}
else {
temp1 *= (pow(u, 2) -
pow((k - 1), 2));
}
++k;
d *= i;
s = floor((n - i) / 2);
y1 += (temp1 / (2 * d)) *
(delta[s][i - 1] +
delta[s - 1][i - 1]);
}
else {
temp2 *= (pow(u, 2) -
pow((l - 1), 2));
++l;
d *= i;
s = floor((n - i) / 2);
y1 += (temp2 / (d)) *
(delta[s][i - 1]);
}
}
cout << y1;
}
int main()
{
int n;
n = 5;
float x[] = { 0, 0.5, 1.0, 1.5, 2.0 };
float fx[] = { 0, 0.191, 0.341, 0.433,
0.477 };
float x1 = 1.22;
Stirling(x, fx, x1, n);
return 0;
}
|
Java
import java.io.*;
import static java.lang.Math.*;
public class A {
static void Stirling(double x[], double fx[],
double x1, int n)
{
double h, a, u, y1 = 0, N1 = 1, d = 1,
N2 = 1, d2 = 1, temp1 = 1,
temp2 = 1, k = 1, l = 1, delta[][];
delta = new double[n][n];
int i, j, s;
h = x[1] - x[0];
s = (int)floor(n / 2);
a = x[s];
u = (x1 - a) / h;
for (i = 0; i < n - 1; ++i) {
delta[i][0] = fx[i + 1] - fx[i];
}
for (i = 1; i < n - 1; ++i) {
for (j = 0; j < n - i - 1; ++j) {
delta[j][i] = delta[j + 1][i - 1]
- delta[j][i - 1];
}
}
y1 = fx[s];
for (i = 1; i <= n - 1; ++i) {
if (i % 2 != 0) {
if (k != 2) {
temp1 *= (pow(u, k) -
pow((k - 1), 2));
}
else {
temp1 *= (pow(u, 2) -
pow((k - 1), 2));
}
++k;
d *= i;
s = (int)floor((n - i) / 2);
y1 += (temp1 / (2 * d)) *
(delta[s][i - 1] +
delta[s - 1][i - 1]);
}
else {
temp2 *= (pow(u, 2) -
pow((l - 1), 2));
++l;
d *= i;
s = (int)floor((n - i) / 2);
y1 += (temp2 / (d)) *
(delta[s][i - 1]);
}
}
System.out.print(+ y1);
}
public static void main(String args[])
{
int n;
n = 5;
double x[] = {0, 0.5, 1.0, 1.5, 2.0 };
double fx[] = {0, 0.191, 0.341, 0.433,
0.477 };
double x1 = 1.22;
Stirling(x, fx, x1, n);
}
}
|
Python3
import math
def Stirling(x, fx, x1, n):
y1 = 0; N1 = 1; d = 1;
N2 = 1; d2 = 1;
temp1 = 1; temp2 = 1;
k = 1; l = 1;
delta = [[0 for i in range(n)]
for j in range(n)];
h = x[1] - x[0];
s = math.floor(n / 2);
a = x[s];
u = (x1 - a) / h;
for i in range(n - 1):
delta[i][0] = fx[i + 1] - fx[i];
for i in range(1, n - 1):
for j in range(n - i - 1):
delta[j][i] = (delta[j + 1][i - 1] -
delta[j][i - 1]);
y1 = fx[s];
for i in range(1, n):
if (i % 2 != 0):
if (k != 2):
temp1 *= (pow(u, k) - pow((k - 1), 2));
else:
temp1 *= (pow(u, 2) - pow((k - 1), 2));
k += 1;
d *= i;
s = math.floor((n - i) / 2);
y1 += (temp1 / (2 * d)) * (delta[s][i - 1] +
delta[s - 1][i - 1]);
else:
temp2 *= (pow(u, 2) - pow((l - 1), 2));
l += 1;
d *= i;
s = math.floor((n - i) / 2);
y1 += (temp2 / (d)) * (delta[s][i - 1]);
print(round(y1, 3));
n = 5;
x = [0, 0.5, 1.0, 1.5, 2.0 ];
fx = [ 0, 0.191, 0.341, 0.433, 0.477];
x1 = 1.22;
Stirling(x, fx, x1, n);
|
C#
using System;
public class A
{
static void Stirling(double[] x, double[] fx,
double x1, int n)
{
double h, a, u, y1 = 0, d = 1, temp1 = 1,
temp2 = 1, k = 1, l = 1;
double[,] delta;
delta = new double[n, n];
int i, j, s;
h = x[1] - x[0];
s = (int)Math.Floor((double)(n / 2));
a = x[s];
u = (x1 - a) / h;
for (i = 0; i < n - 1; ++i)
{
delta[i, 0] = fx[i + 1] - fx[i];
}
for (i = 1; i < n - 1; ++i)
{
for (j = 0; j < n - i - 1; ++j)
{
delta[j, i] = delta[j + 1, i - 1]
- delta[j, i - 1];
}
}
y1 = fx[s];
for (i = 1; i <= n - 1; ++i)
{
if (i % 2 != 0)
{
if (k != 2)
{
temp1 *= (Math.Pow(u, k) -
Math.Pow((k - 1), 2));
}
else
{
temp1 *= (Math.Pow(u, 2) -
Math.Pow((k - 1), 2));
}
++k;
d *= i;
s = (int)Math.Floor((double)((n - i) / 2));
y1 += (temp1 / (2 * d)) *
(delta[s, i - 1] +
delta[s - 1, i - 1]);
}
else
{
temp2 *= (Math.Pow(u, 2) -
Math.Pow((l - 1), 2));
++l;
d *= i;
s = (int)Math.Floor((double)((n - i) / 2));
y1 += (temp2 / (d)) *
(delta[s, i - 1]);
}
}
Console.Write(+ y1);
}
public static void Main()
{
int n;
n = 5;
double[] x = {0, 0.5, 1.0, 1.5, 2.0 };
double[] fx = {0, 0.191, 0.341, 0.433,
0.477 };
double x1 = 1.22;
Stirling(x, fx, x1, n);
}
}
|
PHP
<?php
function Stirling($x, $fx, $x1, $n)
{
$y1 = 0; $N1 = 1;
$d = 1;
$N2 = 1; $d2 = 1; $temp1 = 1; $temp2 = 1;
$k = 1; $l = 1; $delta[$n][$n] = array();
$h = $x[1] - $x[0];
$s = floor($n / 2);
$a = $x[$s];
$u = ($x1 - $a) / $h;
for ($i = 0; $i < $n - 1; ++$i)
{
$delta[$i][0] = $fx[$i + 1] - $fx[$i];
}
for ($i = 1; $i < $n - 1; ++$i)
{
for ($j = 0; $j < $n - $i - 1; ++$j)
{
$delta[$j][$i] = $delta[$j + 1][$i - 1] -
$delta[$j][$i - 1];
}
}
$y1 = $fx[$s];
for ($i = 1; $i <= $n - 1; ++$i)
{
if ($i % 2 != 0)
{
if ($k != 2)
{
$temp1 *= (pow($u, $k) -
pow(($k - 1), 2));
}
else
{
$temp1 *= (pow($u, 2) -
pow(($k - 1), 2));
}
++$k;
$d *= $i;
$s = floor(($n - $i) / 2);
$y1 += ($temp1 / (2 * $d)) *
($delta[$s][$i - 1] +
$delta[$s - 1][$i - 1]);
}
else
{
$temp2 *= (pow($u, 2) -
pow(($l - 1), 2));
++$l;
$d *= $i;
$s = floor(($n - $i) / 2);
$y1 += ($temp2 / ($d)) *
($delta[$s][$i - 1]);
}
}
echo $y1;
}
$n = 5;
$x = array(0, 0.5, 1.0, 1.5, 2.0 );
$fx = array( 0, 0.191, 0.341, 0.433,
0.477 );
$x1 = 1.22;
Stirling($x, $fx, $x1, $n);
?>
|
Javascript
function Stirling(x, fx, x1, n)
{
let h, a, u, y1 = 0, N1 = 1, d = 1,
N2 = 1, d2 = 1, temp1 = 1, temp2 = 1,
k = 1, l = 1;
let i, j, s;
let delta = [];
for (i = 0; i < n; i++)
delta.push(new Array(n));
h = x[1] - x[0];
s = Math.floor(n / 2);
a = x[s];
u = (x1 - a) / h;
for (i = 0; i < n - 1; ++i) {
delta[i][0] = fx[i + 1] - fx[i];
}
for (i = 1; i < n - 1; ++i) {
for (j = 0; j < n - i - 1; ++j) {
delta[j][i] = delta[j + 1][i - 1]
- delta[j][i - 1];
}
}
y1 = fx[s];
for (i = 1; i <= n - 1; ++i) {
if (i % 2 != 0) {
if (k != 2) {
temp1 *= (Math.pow(u, k) -
Math.pow((k - 1), 2));
}
else {
temp1 *= (Math.pow(u, 2) -
Math.pow((k - 1), 2));
}
++k;
d *= i;
s = Math.floor((n - i) / 2);
y1 += (temp1 / (2 * d)) *
(delta[s][i - 1] +
delta[s - 1][i - 1]);
}
else {
temp2 *= (Math.pow(u, 2) -
Math.pow((l - 1), 2));
++l;
d *= i;
s = Math.floor((n - i) / 2);
y1 += (temp2 / (d)) *
(delta[s][i - 1]);
}
}
console.log(y1.toFixed(3));
}
let n = 5;
let x = [ 0, 0.5, 1.0, 1.5, 2.0 ];
let fx = [ 0, 0.191, 0.341, 0.433,
0.477 ];
let x1 = 1.22;
Stirling(x, fx, x1, n);
|
Time complexity: O(n2) where n is no of given floating values
Auxiliary space: O(1)
The main advantage of Stirling’s formula over other similar formulas is that it decreases much more rapidly than other difference formula hence considering first few number of terms itself will give better accuracy, whereas it suffers from a disadvantage that for Stirling approximation to be applicable there should be a uniform difference between any two consecutive x.
Reference – Higher Engineering Mathematics by B.S. Grewal.
Share your thoughts in the comments
Please Login to comment...