Program to find HCF iteratively

HCF (Highest Common Factor) or GCD (Greatest Common Divisor) of two numbers is the largest number that divides both of them. 

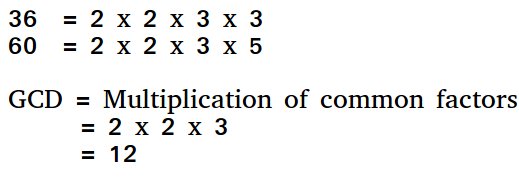For example, GCD of 20 and 28 is 4, and GCD of 98 and 56 is 14.

We have discussed the recursive solution in the below post. Recursive program to find GCD or HCF of two numbers
Below is the iterative implementation of Euclid’s algorithm 

C++

// C++ program to find HCF of two
// numbers iteratively.
#include <bits/stdc++.h>
using namespace std;

int hcf(int a, int b)
{
    if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b) {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}

// Driver code
int main()
{
    int a = 60, b = 96;
    cout << hcf(a, b) << endl;
    return 0;
}

// This code is contributed by shubhamsingh10

C

// C program to find HCF of two
// numbers iteratively.
#include <stdio.h>

int hcf(int a, int b)
{
    if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b) {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}
int main()
{
    int a = 60, b = 96;
    printf("%d\n", hcf(a, b));
    return 0;
}

Java

// JAVA Code for Program to find
// HCF iteratively
import java.util.*;

class GFG {

    static int hcf(int a, int b)
    {
        if (a == 0)
            return b;
        else if (b == 0)
            return a;
        while (a != b) {
            if (a > b)
                a = a - b;
            else
                b = b - a;
        }
        return a;
    }

    /* Driver program */
    public static void main(String[] args)
    {
        int a = 60, b = 96;
        System.out.println(hcf(a, b));
    }
}

// This code is contributed by Arnav Kr. Mandal.

Python3

// Python program to find HCF of two
// numbers iteratively.


def hcf(a, b):
    if(a == 0):
      return b
    else if(b == 0):
      return a
    while (a != b):
        if (a > b):
            a = a - b
        else:
            b = b - a
    return a


a = 60
b = 96
print(hcf(a, b))

C#

// C# Code for Program to find
// HCF iteratively
using System;

class GFG {

    static int hcf(int a, int b)
    {
        if (a == 0)
            return b;
        else if (b == 0)
            return a;
        while (a != b) {
            if (a > b)
                a = a - b;
            else
                b = b - a;
        }
        return a;
    }

    // Driver program
    public static void Main()
    {
        int a = 60, b = 96;
        Console.WriteLine(hcf(a, b));
    }
}

// This code is contributed by vt_m.

PHP

<?php
//PHP program to find HCF of two
// numbers iteratively.

function hcf($a, $b)
{   if($a==0)
      return $b;
   else if($b==0)
      return $a;
    while ($a != $b) {
        if ($a > $b)
            $a = $a - $b;
        else
            $b = $b - $a;
    }

    return $a;
}

// Driver code
$a = 60; $b = 96;
echo hcf($a, $b), "\n";

// This code is contributed by ajit
?>

Javascript

<script>

//Javascript program to find HCF of two
// numbers iteratively.

function hcf(a, b)
{   if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b)
    {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}

// Driver code
    let a = 60, b = 96;
    document.write(hcf(a, b) + "<br>");

// This code is contributed by Mayank Tyagi

</script>

Output: 

12

Time Complexity: O(max(a, b))

Auxiliary Space: O(1)