Problem solving on Boolean Model and Vector Space Model
Last Updated :
30 May, 2021
Boolean Model:
It is a simple retrieval model based on set theory and boolean algebra. Queries are designed as boolean expressions which have precise semantics. Retrieval strategy is based on binary decision criterion. Boolean model considers that index terms are present or absent in a document.
Problem Solving:
Consider 5 documents with a vocabulary of 6 terms
- document 1 = ‘ term1 term3 ‘
- document 2 = ‘ term 2 term4 term6 ‘
- document 3 = ‘ term1 term2 term3 term4 term5 ‘
- document 4 = ‘ term1 term3 term6 ‘
- document 5 = ‘ term3 term4 ‘
Our documents in boolean model
| | term 1 | term 2 | term 3 | term 4 | term 5 | term 6 |
| document 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| document 2 | 0 | 1 | 0 | 1 | 0 | 1 |
| document 3 | 1 | 1 | 1 | 1 | 1 | 0 |
| document 4 | 1 | 0 | 1 | 0 | 0 | 1 |
| document 5 | 0 | 0 | 1 | 1 | 0 | 0 |
Consider the query
Find the document consisting of term1 and term3 and not term2
term1 ∧ term3 ∧ ¬ term2
| | term1 | ¬term 2 | term 3 | term 4 | term 5 | term 6 |
| document 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| document 2 | 0 | 0 | 0 | 1 | 0 | 1 |
| document 3 | 1 | 0 | 1 | 1 | 1 | 0 |
| document 4 | 1 | 1 | 1 | 0 | 0 | 1 |
| document 5 | 0 | 1 | 1 | 1 | 0 | 0 |
- document 1 : 1 ∧ 1∧ 1 = 1
- document 2 : 0 ∧ 0 ∧ 0 = 0
- document 3 : 1 ∧ 1 ∧ 0 = 0
- document 4 : 1 ∧ 1 ∧ 1 = 1
- document 5 : 0 ∧ 1 ∧ 1 = 0
Based on the above computation document1 and document4 are relevant to the given query
Vector Model:
The method of performing the operations and the formulas required for the computation is present in the previous document that is part 1. Consider the following collection of documents.
- document1 = ‘one two ‘
- document2 = ‘three two four ‘
- document3 =’one two three ‘
- document4 =’one two ‘
The formulas used
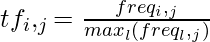
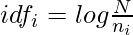

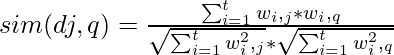
Some terms appear thrice, twice and sometimes only once in the document.The total number of documents N=4. Therefore, the IDF values of the terms are:
one --> log2(4/3) = 0.4147
two --> log2(4/4) = 0
three --> log2(4/2) = 1
four -->log2(4/1) = 2
Representation in boolean model
| | one | two | three | four |
| document1 | 1 | 1 | 0 | 0 |
| document2 | 0 | 1 | 1 | 1 |
| document3 | 1 | 1 | 1 | 0 |
| document4 | 1 | 1 | 0 | 0 |
Calculation of term frequency
one --> 3/4 = 0.75
two --> 4/4 = 1
three --> 2/4 = 0.5
four --> 1/4 = 0.25
Calculation of weights ( tf * idf )
weight(one) --> 0.75 * 0.4147 = 0.3110
weight(two) --> 1 * 0 = 0
weight(three) --> 0.5 * 1 = 0.5
weight(four) --> 0.25 * 2 = 0.5
Representation of vector model in terms of weights
| | one | two | three | four |
| document1 | 0.3110 | 0 | 0 | 0 |
| document2 | 0 | 0 | 0.5 | 0.5 |
| document3 | 0.3110 | 0 | 0.5 | 0 |
| document4 | 0.3110 | 0 | 0 | 0 |
QUERY: Document containing ‘ one three three ‘
Calculation of weights for query terms(term frequency)
- weight(one) –> 1/3 = 0.333
- weight(three) –> 2/3 = 0.667
Vector representation
- Document
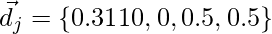
- Query
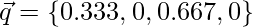
Similarity calculation: the

Ranking of the documents, ( for ranking we have followed the method in statistics for the case of allocating same rank to two different items)
| document1 | 2nd |
| document2 | 4th |
| document3 | 1st |
| document4 | 2nd |
Since the similarity between document 3 is greater than the similarities between the other documents, 3rd document is more relevant to the query.
Share your thoughts in the comments
Please Login to comment...