Probability of distributing M items among X bags such that first bag contains N items

Given three integers N, M, X. The task is to find the probability of distributing M items among X bags such that first bag contains N items

Examples:

Input : M = 7, X =3, N = 3 
Output : 0.2 
The Number of ways to keep 7 items in 3 bags is .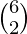 
The Number of ways to keep 4 items in 2 bags is 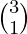. As the first bag contains 3 items. 
The probability is /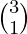

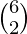
Input : M = 9, X = 3, N = 4 
Output : 0.142857 

Approach :
In general, the Number of ways to place N items in K bags is .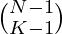 

• The Number of ways to keep M items in X bags is .
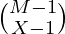• The Number of ways to keep (M-N) items in (X-1) bags is 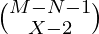. As the first bag contains N items.
• The probability is /.

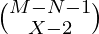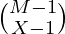Below is the implementation of the above approach:

C++

// CPP program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
#include <bits/stdc++.h>
using namespace std;

// Function to find factorial of a number
int factorial(int n)
{
    if (n <= 1)
        return 1;
    return n * factorial(n - 1);
}

// Function to find nCr
int nCr(int n, int r)
{
    return factorial(n) / (factorial(r) * factorial(n - r));
}

// Function to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
float Probability(int M, int N, int X)
{
    return (float)(nCr(M - N - 1, X - 2) /
                    (nCr(M - 1, X - 1) * 1.0));
}

// Driver code
int main()
{
    int M = 9, X = 3, N = 4;

    // Function call
    cout << Probability(M, N, X);

    return 0;
}

Java

// Java program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags

class GFG
{

    // Function to find factorial of a number
    public static int factorial(int n)
    {
        if (n <= 1)
            return 1;

        return n * factorial(n - 1);
    }

    // Function to find nCr
    public static int nCr(int n, int r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }

    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    public static float Probability(int M, int N, int X)
    {
        return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }

    // Driver code
    public static void main(String[] args)
    {
        int M = 9, X = 3, N = 4;

        // Function call
        System.out.println(Probability(M, N, X));
    }
}

// This code is contributed by
// sanjeev2552

Python3

# Python3 program to find probability of
# first bag to contain N items such
# that M items are distributed among X bags

# Function to find factorial of a number
def factorial(n) :

    if (n <= 1) :
        return 1;

    return n * factorial(n - 1);

# Function to find nCr
def nCr(n, r) :

    return (factorial(n) / (factorial(r) *
                            factorial(n - r)));

# Function to find probability of
# first bag to contain N items such
# that M items are distributed among X bags
def Probability(M, N, X) :

    return float(nCr(M - N - 1, X - 2) /
                (nCr(M - 1, X - 1) * 1.0));

# Driver code
if __name__ == "__main__" :

    M = 9; X = 3; N = 4;

    # Function call
    print(Probability(M, N, X));

# This code is contributed by AnkitRai01

C#

// C# program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
using System;

class GFG
{

    // Function to find factorial of a number
    static int factorial(int n)
    {
        if (n <= 1)
            return 1;

        return n * factorial(n - 1);
    }

    // Function to find nCr
    static int nCr(int n, int r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }

    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    static float Probability(int M, int N, int X)
    {
        return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }

    // Driver code
    static void Main()
    {
        int M = 9, X = 3, N = 4;

        // Function call
        Console.WriteLine(Probability(M, N, X));
    }
}

// This code is contributed by
// mohitkumar 29

Javascript

<script>
// Java Script program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags


    // Function to find factorial of a number
    function factorial( n)
    {
        if (n <= 1)
            return 1;

        return n * factorial(n - 1);
    }

    // Function to find nCr
    function nCr( n,  r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }

    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    function Probability(M,N,X)
    {
        return parseFloat(nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }

    // Driver code
    let M = 9, X = 3, N = 4;

        // Function call
        document.write(Probability(M, N, X).toFixed(6));
// This code is contributed by Bobby
</script>

Output:

0.142857

Time Complexity: O(n), time taken by the algorithm is linear as the recursion runs for n times
Auxiliary Space: O(n) due to the recursive call stack, In worst case the stack will contain all recursive calls till n becomes 0 hence the space taken by the algorithm is linear