Print Left View of a Binary Tree

Given a Binary Tree, the task is to print the left view of the Binary Tree. The left view of a Binary Tree is a set of leftmost nodes for every level.

Examples:

Input: 
                   4
                /   \
              5     2
                   /   \
                3     1
              /  \
           6    7

Output: 4 5 3 6
Explanation:

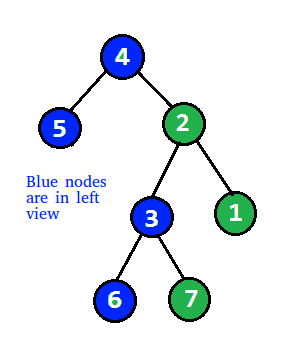
Input:
         1
      /   \
    2       3
      \   
       4  
         \
          5
            \
             6
Output: 1 2 4 5 6

Print Left View of a Binary Tree Using Recursion: 

Keep track of the level of a node by passing the level as a parameter to all recursive calls and also keep track of the maximum level. Whenever, we see a node whose level is more than maximum level so far, we print the node because this is the first node in its level 

Note: We traverse the left subtree before right subtree. 

Below is the implementation of the above idea.

C++

// C++ program to print left view of Binary Tree
#include <bits/stdc++.h>
using namespace std;

struct Node {
    int data;
    struct Node *left, *right;
};

// A utility function to
// create a new Binary Tree Node
struct Node* newNode(int item)
{
    struct Node* temp
        = (struct Node*)malloc(sizeof(struct Node));
    temp->data = item;
    temp->left = temp->right = NULL;
    return temp;
}

// Recursive function to print
// left view of a binary tree.
void leftViewUtil(struct Node* root, int level,
                  int* max_level)
{
    // Base Case
    if (root == NULL)
        return;

    // If this is the first Node of its level
    if (*max_level < level) {
        cout << root->data << " ";
        *max_level = level;
    }

    // Recur for left subtree first,
    // then right subtree
    leftViewUtil(root->left, level + 1, max_level);
    leftViewUtil(root->right, level + 1, max_level);
}

// A wrapper over leftViewUtil()
void leftView(struct Node* root)
{
    int max_level = 0;
    leftViewUtil(root, 1, &max_level);
}

// Driver Code
int main()
{
    Node* root = newNode(10);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(7);
    root->left->right = newNode(8);
    root->right->right = newNode(15);
    root->right->left = newNode(12);
    root->right->right->left = newNode(14);

    leftView(root);

    return 0;
}

C

// C program to print left view of Binary Tree
#include <stdio.h>
#include <stdlib.h>

struct node {
    int data;
    struct node *left, *right;
};

// A utility function to create a new Binary Tree node
struct node* newNode(int item)
{
    struct node* temp
        = (struct node*)malloc(sizeof(struct node));
    temp->data = item;
    temp->left = temp->right = NULL;
    return temp;
}

// Recursive function to print left view of a binary tree.
void leftViewUtil(struct node* root, int level,
                  int* max_level)
{
    // Base Case
    if (root == NULL)
        return;

    // If this is the first node of its level
    if (*max_level < level) {
        printf("%d ", root->data);
        *max_level = level;
    }

    // Recur for left and right subtrees
    leftViewUtil(root->left, level + 1, max_level);
    leftViewUtil(root->right, level + 1, max_level);
}

// A wrapper over leftViewUtil()
void leftView(struct node* root)
{
    int max_level = 0;
    leftViewUtil(root, 1, &max_level);
}

// Driver code
int main()
{
    struct node* root = newNode(10);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(7);
    root->left->right = newNode(8);
    root->right->right = newNode(15);
    root->right->left = newNode(12);
    root->right->right->left = newNode(14);

    leftView(root);

    return 0;
}

Java

// Java program to print left view of binary tree

/* Class containing left and right child of current
node and key value*/
class Node {
    int data;
    Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

/* Class to print the left view */
class BinaryTree {
    Node root;
    static int max_level = 0;

    // recursive function to print left view
    void leftViewUtil(Node node, int level)
    {
        // Base Case
        if (node == null)
            return;

        // If this is the first node of its level
        if (max_level < level) {
            System.out.print(node.data + " ");
            max_level = level;
        }

        // Recur for left and right subtrees
        leftViewUtil(node.left, level + 1);
        leftViewUtil(node.right, level + 1);
    }

    // A wrapper over leftViewUtil()
    void leftView()
    {
        max_level = 0;
        leftViewUtil(root, 1);
    }

    /* testing for example nodes */
    public static void main(String args[])
    {
        /* creating a binary tree and entering the nodes */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(7);
        tree.root.left.right = new Node(8);
        tree.root.right.right = new Node(15);
        tree.root.right.left = new Node(12);
        tree.root.right.right.left = new Node(14);

        tree.leftView();
    }
}

Python3

# Python program to print left view of Binary Tree

# A binary tree node
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


# Recursive function print left view of a binary tree
def leftViewUtil(root, level, max_level):

    # Base Case
    if root is None:
        return

    # If this is the first node of its level
    if (max_level[0] < level):
        print (root.data, end = " ")
        max_level[0] = level

    # Recur for left and right subtree
    leftViewUtil(root.left, level + 1, max_level)
    leftViewUtil(root.right, level + 1, max_level)


# A wrapper over leftViewUtil()
def leftView(root):
    max_level = [0]
    leftViewUtil(root, 1, max_level)


# Driver program to test above function
if __name__ == '__main__':
    root = Node(10)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(7)
    root.left.right = Node(8)
    root.right.right = Node(15)
    root.right.left = Node(12)
    root.right.right.left = Node(14)

    leftView(root)

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

using System;

// C# program to print left view of binary tree

/* Class containing left and right child of current
node and key value*/
public class Node {
    public int data;
    public Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

/* Class to print the left view */
public class BinaryTree {
    public Node root;
    public static int max_level = 0;

    // recursive function to print left view
    public virtual void leftViewUtil(Node node, int level)
    {
        // Base Case
        if (node == null) {
            return;
        }

        // If this is the first node of its level
        if (max_level < level) {
            Console.Write(node.data + " ");
            max_level = level;
        }

        // Recur for left and right subtrees
        leftViewUtil(node.left, level + 1);
        leftViewUtil(node.right, level + 1);
    }

    // A wrapper over leftViewUtil()
    public virtual void leftView()
    {
        leftViewUtil(root, 1);
    }

    /* testing for example nodes */
    public static void Main(string[] args)
    {
        /* creating a binary tree and entering the nodes */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(7);
        tree.root.left.right = new Node(8);
        tree.root.right.right = new Node(15);
        tree.root.right.left = new Node(12);
        tree.root.right.right.left = new Node(14);

        tree.leftView();
    }
}

// This code is contributed by Shrikant13

Javascript

<script>

// Javascript program to print left view
// of binary tree

// Class containing left and right
// child of current node and key value
class Node
{
    constructor(item)
    {
        this.data = item;
        this.left = null;
        this.right = null;
    }
}

// Class to print the left view
var root ;
var max_level = 0;

// Recursive function to print left view
function leftViewUtil(node, level)
{

    // Base Case
    if (node == null)
    {
        return;
    }

    // If this is the first node of its level
    if (max_level < level)
    {
        document.write(" " + node.data);
        max_level = level;
    }

    // Recur for left and right subtrees
    leftViewUtil(node.left, level + 1);
    leftViewUtil(node.right, level + 1);
}

// A wrapper over leftViewUtil()
function leftView()
{
    leftViewUtil(root, 1);
}

// Driver code

// Testing for example nodes
// Creating a binary tree and
// entering the nodes
root = Node(10)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(7)
root.left.right = new Node(8)
root.right.right = new Node(15)
root.right.left = new Node(12)
root.right.right.left = new Node(14)


leftView();

// This code is contributed by rrrtnx

</script>

Output

10 2 7 14 

Time Complexity: O(N), The function does a simple traversal of the tree, so the complexity is O(n). 
Auxiliary Space: O(h), due to the stack space during recursive call. ‘h’ here is the height of the binary tree.

Print Left View of a Binary Tree Using Level Order Traversal:

Below is the idea to solve the problem:

The left view contains all nodes that are the first nodes in their levels. A simple solution is to do level order traversal and print the first node in every level. 

Follow the below step to Implement the idea:

• Do level order traversal of the tree.
  • For each level keep a track of the current level and print the first encountered node of this level.
  • Move to the next level.

Below is the implementation of the above approach:

C++

// C++ program to print left view of
// Binary Tree

#include<bits/stdc++.h>
using namespace std;

// A Binary Tree Node
struct Node
{
    int data;
    struct Node *left, *right;
};

// Utility function to create a new tree node
Node* newNode(int data)
{
    Node *temp = new Node;
    temp->data = data;
    temp->left = temp->right = NULL;
    return temp;
}

// function to print left view of
// binary tree
void printLeftView(Node* root)
{
    if (!root)
        return;

    queue<Node*> q;
    q.push(root);

    while (!q.empty())
    {
        // number of nodes at current level
        int n = q.size();

        // Traverse all nodes of current level
        for(int i = 1; i <= n; i++)
        {
            Node* temp = q.front();
            q.pop();

            // Print the left most element
            // at the level
            if (i == 1)
                cout<<temp->data<<" ";

            // Add left node to queue
            if (temp->left != NULL)
                q.push(temp->left);

            // Add right node to queue
            if (temp->right != NULL)
                q.push(temp->right);
        }
    }
}

// Driver code
int main()
{
    // Let's construct the tree as
    // shown in example

    Node* root = newNode(10);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(7);
    root->left->right = newNode(8);
    root->right->right = newNode(15);
    root->right->left = newNode(12);
    root->right->right->left = newNode(14);

    printLeftView(root);
}

// This code is contributed by
// Manne SreeCharan

Java

// Java program to print left view of Binary
// Tree
import java.util.*;

public class PrintRightView {
    // Binary tree node
    private static class Node {
        int data;
        Node left, right;

        public Node(int data)
        {
            this.data = data;
            this.left = null;
            this.right = null;
        }
    }

    // function to print left view of binary tree
    private static void printLeftView(Node root)
    {
        if (root == null)
            return;

        Queue<Node> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            // number of nodes at current level
            int n = queue.size();

            // Traverse all nodes of current level
            for (int i = 1; i <= n; i++) {
                Node temp = queue.poll();

                // Print the left most element at
                // the level
                if (i == 1)
                    System.out.print(temp.data + " ");

                // Add left node to queue
                if (temp.left != null)
                    queue.add(temp.left);

                // Add right node to queue
                if (temp.right != null)
                    queue.add(temp.right);
            }
        }
    }

    // Driver code
    public static void main(String[] args)
    {
        // construct binary tree as shown in
        // above diagram
        Node root = new Node(10);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(7);
        root.left.right = new Node(8);
        root.right.right = new Node(15);
        root.right.left = new Node(12);
        root.right.right.left = new Node(14);

        printLeftView(root);
    }
}

// This code is contributed by
// Manne SreeCharan

Python3

# Python3 program to print left view of
# Binary Tree

# Binary Tree Node
""" utility that allocates a newNode
with the given key """


class newNode:

    # Construct to create a newNode
    def __init__(self, key):
        self.data = key
        self.left = None
        self.right = None
        self.hd = 0

# function to print left view of
# binary tree


def printLeftView(root):

    if (not root):
        return

    q = []
    q.append(root)

    while (len(q)):

        # number of nodes at current level
        n = len(q)

        # Traverse all nodes of current level
        for i in range(1, n + 1):
            temp = q[0]
            q.pop(0)

            # Print the left most element
            # at the level
            if (i == 1):
                print(temp.data, end=" ")

            # Add left node to queue
            if (temp.left != None):
                q.append(temp.left)

            # Add right node to queue
            if (temp.right != None):
                q.append(temp.right)


# Driver Code
if __name__ == '__main__':

    root = newNode(10)
    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(7)
    root.left.right = newNode(8)
    root.right.right = newNode(15)
    root.right.left = newNode(12)
    root.right.right.left = newNode(14)
    printLeftView(root)

# This code is contributed by
# Manne SreeCharan

C#

// C# program to print left view
// of Binary Tree
using System;
using System.Collections.Generic;

public class PrintRightView {
    // Binary tree node
    private class Node {
        public int data;
        public Node left, right;

        public Node(int data)
        {
            this.data = data;
            this.left = null;
            this.right = null;
        }
    }

    // function to print left view of binary tree
    private static void printRightView(Node root)
    {
        if (root == null)
            return;

        Queue<Node> queue = new Queue<Node>();
        queue.Enqueue(root);

        while (queue.Count != 0) {
            // number of nodes at current level
            int n = queue.Count;

            // Traverse all nodes of current level
            for (int i = 1; i <= n; i++) {
                Node temp = queue.Dequeue();

                // Print the left most element at
                // the level
                if (i == 1)
                    Console.Write(temp.data + " ");

                // Add left node to queue
                if (temp.left != null)
                    queue.Enqueue(temp.left);

                // Add right node to queue
                if (temp.right != null)
                    queue.Enqueue(temp.right);
            }
        }
    }

    // Driver code
    public static void Main(String[] args)
    {
        // construct binary tree as shown in
        // above diagram
        Node root = new Node(10);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(7);
        root.left.right = new Node(8);
        root.right.right = new Node(15);
        root.right.left = new Node(12);
        root.right.right.left = new Node(14);
        printRightView(root);
    }
}

// This code is contributed Manne SreeCharan

Javascript

<script>

// JavaScript program to print left view of
// Binary Tree
class newNode{

    // Construct to create a newNode
    constructor(key){
        this.data = key
        this.left = null
        this.right = null
        this.hd = 0
    }
}

// function to print left view of
// binary tree
function printLeftView(root){

    if (root == null)
        return

    let q = []
    q.push(root)

    while (q.length){

        // number of nodes at current level
        let n = q.length

        // Traverse all nodes of current level
        for(let i=1;i< n + 1;i++){
            let temp = q.shift()

            // Print the left most element
            // at the level
            if (i == 1)
                document.write(temp.data," ")

            // Add left node to queue
            if (temp.left != null)
                q.push(temp.left)

            // Add right node to queue
            if (temp.right != null)
                q.push(temp.right)
        }
    }
}

// Driver Code
let root = new newNode(10)
root.left = new newNode(2)
root.right = new newNode(3)
root.left.left = new newNode(7)
root.left.right = new newNode(8)
root.right.right = new newNode(15)
root.right.left = new newNode(12)
root.right.right.left = new newNode(14)
printLeftView(root)

// This code is contributed by shinjanpatra

</script>

Output

10 2 7 14 

Time Complexity: O(N), where n is the number of nodes in the binary tree.
Auxiliary Space: O(N) since using space for auxiliary queue

Print Left View of a Binary Tree Using queue and a null pointer:

Below is the idea to solve the problem:

Use queue and a null pointer to mark the first element of each level. Insert a null pointer in the first and as the null pointer is reached mark bool as true and take the next element as left view element.

Below is the Implementation of the above approach:

C++

// C++ Code for the above iterative approach
#include <bits/stdc++.h>
using namespace std;

//  Tree Node Structure contains data, left and right
//  pointer
struct Node {
    int data;
    struct Node *left, *right;
};

// A utility function to
// create a new Binary Tree Node
struct Node* newNode(int item)
{
    struct Node* temp
        = (struct Node*)malloc(sizeof(struct Node));
    temp->data = item;
    temp->left = temp->right = NULL;
    return temp;
}

// function to get the left view of binary tree in vector
vector<int> leftView(Node* root)
{

    // store the left view
    vector<int> ans;

    // Base Case : Empty Tree
    if (!root)
        return ans;


    // Create an empty queue and enque root node and null
    queue<Node*> q;
    q.push(root);
    q.push(NULL);
    bool ok = true;

    // Traverse till queue is not empty
    while (!q.empty()) {
        // get the front node and dequeue it from queue
        auto it = q.front();
        q.pop();

        // if the front node is null do following steps
        if (it == NULL) {
            if (ok == false)
                ok = true;


            if (q.size() == 0)
                break;

            else
                q.push(NULL);

        }
        // else do the following steps
        else {
            if (ok) {
                ans.push_back(it->data);
                ok = false;
            }

            if (it->left)
                q.push(it->left);

            if (it->right)
                q.push(it->right);

        }
    }

    // return the left view
    return ans;
}

// driver code to test above code on a test case
int main()
{
    /*
    Input :
                   10
                 /    \
                2      3
               / \    / \
              7   8  12  15
                         /
                        14

     Output : 10 2 7 14
  */
    // let's build above shown tree
    Node* root = newNode(10);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(7);
    root->left->right = newNode(8);
    root->right->right = newNode(15);
    root->right->left = newNode(12);
    root->right->right->left = newNode(14);

    // call leftview function and store output in vec
    vector<int> vec = leftView(root);
    // traverse on left view and print each element
    for (int x : vec)
        cout << x << " ";
    cout << endl;

    return 0;
}

// This code is updated by Tapesh(tapeshdua420)

Java

// Java Program to print the left view
import java.util.*;

class GFG {
    // Binary Tree Node
    static class Node {
        int data;
        Node left, right;

        public Node(int item)
        {
            data = item;
            left = right = null;
        }
    };
    // function to print the left view of binary tree
    public static ArrayList<Integer> leftView(Node root)
    {
        // Your code here
        ArrayList<Integer> ans = new ArrayList<>();

        if (root == null) {
            return ans;
        }

        Queue<Node> q = new LinkedList<>();
        q.add(root);
        q.add(null);
        boolean ok = true;

        while (!q.isEmpty()) {
            Node it = q.poll();
            if (it == null) {
                if (ok == false) {
                    ok = true;
                }

                if (q.size() == 0)
                    break;

                else {
                    q.add(null);
                }
            }
            else {

                if (ok) {
                    ans.add(it.data);
                    ok = false;
                }

                if (it.left != null) {
                    q.add(it.left);
                }

                if (it.right != null) {
                    q.add(it.right);
                }
            }
        }

        return ans;
    }
    // driver code
    public static void main(String[] args)
    {
        Node root = new Node(10);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(7);
        root.left.right = new Node(8);
        root.right.right = new Node(15);
        root.right.left = new Node(12);
        root.right.right.left = new Node(14);

        ArrayList<Integer> vec = leftView(root);
        for (int x : vec) {
            System.out.print(x + " ");
        }
        System.out.println();
    }
}

// This code is contributed by Tapesh(tapeshdua420)

Python3

# Python Program to print left view

# Tree Node Class
class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# function to get the left view of binary tree
def leftView(root):
    ans = []

    if not root:
        return ans

    q = []
    q.append(root)
    q.append(None)
    ok = True

    while len(q) != 0:
        it = q[0]
        del q[0]
        if it == None:
            if ok == False:
                ok = True
            if len(q) == 0:
                break

            else:
                q.append(None)

        else:
            if ok:
                ans.append(it.data)
                ok = False

            if it.left != None:
                q.append(it.left)
            if it.right != None:
                q.append(it.right)

    return ans


# Driver Code
if __name__ == '__main__':
    root = Node(10)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(7)
    root.left.right = Node(8)
    root.right.right = Node(15)
    root.right.left = Node(12)
    root.right.right.left = Node(14)

    vec = leftView(root)

    # print the left view
    for x in vec:
        print(x, end=" ")
    print()

# This code is contributed by Tapesh(tapeshdua420)

C#

// C# program to print the left view of binary tree
using System;
using System.Collections.Generic;

class GFG {
    // Binary Tree Node
    public class Node {
        public int data;
        public Node left, right;

        public Node(int item)
        {
            data = item;
            left = right = null;
        }
    };
    // function to print the left view of binary tree
    public static List<int> leftView(Node root)
    {
        // Your code here
        List<int> ans = new List<int>();
        if (root == null) {
            return ans;
        }
        Queue<Node> q = new Queue<Node>();
        q.Enqueue(root);
        q.Enqueue(null);
        bool ok = true;
        while (q.Count != 0) {
            Node it = q.Dequeue();
            if (it == null) {
                if (ok == false) {
                    ok = true;
                }
                if (q.Count == 0)
                    break;
                else {
                    q.Enqueue(null);
                }
            }
            else {
                if (ok) {
                    ans.Add(it.data);
                    ok = false;
                }
                if (it.left != null) {
                    q.Enqueue(it.left);
                }
                if (it.right != null) {
                    q.Enqueue(it.right);
                }
            }
        }
        return ans;
    }
    // driver code
    public static void Main()
    {
        Node root = new Node(10);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(7);
        root.left.right = new Node(8);
        root.right.right = new Node(15);
        root.right.left = new Node(12);
        root.right.right.left = new Node(14);
        List<int> vec = leftView(root);
        foreach(var x in vec) Console.Write(x + " ");
        Console.WriteLine();
    }
}

// This code is contributed by Tapesh(tapeshdua420)

Output

10 2 7 14 

Time Complexity: O(N) where N is the total number of nodes.
Auxiliary Space: O(N) due to the space occupied by queue.