Prepositional Inference in Artificial Intelligence

Last Updated : 11 Jul, 2023

Let’s start with quantifiers that are universal. Assume we have in our knowledge base the conventional folklore axiom that All Greedy Kings Are Bad:

$\forall x \operatorname{King}(x) \wedge \operatorname{Greed} y(x) \Rightarrow \operatorname{Evil}(x)$

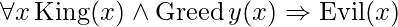
Then it appears that inferring any of the following sentences is perfectly acceptable:

$\operatorname{King}(J o h n) \wedge \operatorname{Greed} y(J o h n) \Rightarrow \operatorname{Evil}(J o h n)$
$\text { King }(\text { Richard }) \wedge \text { Greedy }(\text { Richard }) \Rightarrow \text { Evil }(\text { Richard })$
$\text { King }(\text { Father }(J o h n)) \wedge \text { Greedy }(\text { Father }(J o h n)) \Rightarrow \operatorname{Evil}(\text { Father }(J o h n))$

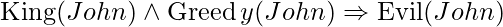
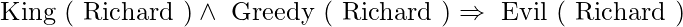
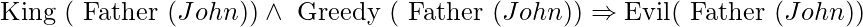
Universal Instantiation

The Universal Instantiation (UI) rule states that by replacing a ground word (a term without variables) for the variable, we can infer any sentence. We employ the notion of replacements to formalize the inference rule. Let 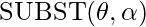$\operatorname{SUBST}(\theta, \alpha)$ denote the result of putting the substitution 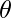$\theta$ to work on the sentence 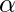$\alpha$ . The rule is then expressed as \frac{\forall v \alpha}{\operatorname{SUBST}(\{v / g\}, \alpha)}.

For every variable 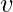$v$ and ground term 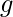$g$ . For example, the substitutions

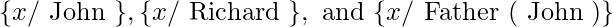$\{x / \text { John }\},\{x / \text { Richard }\}, \text { and }\{x / \text { Father }(\text { John })\}$ get the three phrases shown above.

Existential Instantiation

The variable is substituted by a single new constant symbol in the Existential Instantiation rule. In the knowledge base 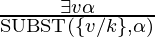$\frac{\exists v \alpha}{\operatorname{SUBST}(\{v / k\}, \alpha)}$ , for any sentence, variable v, and constant symbol k that does not appear elsewhere

For example, if 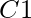$C1$ does not appear elsewhere in the knowledge base, we can infer the sentence 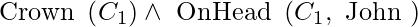$\text { Crown }\left(C_{1}\right) \wedge \text { OnHead }\left(C_{1}, \text { John }\right)$ from the sentence \text { Crown }\left(C_{1}\right) \wedge \text { OnHead }\left(C_{1}, J o h n\right). Essentially, an existential sentence states that some item satisfies a condition, and the existential instantiation rule simply names that object. Of course, that name can’t be used for another object. Consider the following scenario: assume we uncover a number that is slightly larger than 2.71828 and fulfils the equation 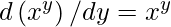$d\left(x^{y}\right) / d y=x^{y}$ for x. We can give this number a name, such as 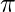$\pi$ , but giving it the name of an existent object, such as, would be a mistake. The new name is known as a Skolem constant in logic. Existential Instantiation is a subset of the broader skolemization process. Existential instantiation is a special case of Skolemization process.

Unlike Universal Instantiation, which can be used multiple times to yield a variety of results, Existential Instantiation can only be used once and then the existentially quantified statement can be deleted. For example, once we’ve inserted the sentence 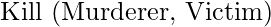$\text { Kill (Murderer, Victim) }$ , we don’t require 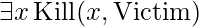$\exists x \operatorname{Kill}(x, \operatorname{Victim})$ . The new knowledge base is not strictly speaking logically equivalent to the old, but it can be proved to be inferentially identical in the sense that it is satisfiable exactly when the old knowledge base is satisfiable.