POTD Solutions | 22 Oct’ 23 | Number of paths

View all POTD Solutions

Welcome to the daily solutions of our PROBLEM OF THE DAY (POTD). We will discuss the entire problem step-by-step and work towards developing an optimized solution. This will not only help you brush up on your concepts of Combinatorics but will also help you build up problem-solving skills.

POTD 22 October: Number of paths

Given an MxN matrix, The task is to count all the possible paths from the top left to the bottom right of an MxN matrix with the constraint that from each cell you can either move to the right or down. Return answer modulo 10⁹+ 7.

Number of paths using Combinatorics

The Idea is to use Combinatorics.

Total number of moves in which we have to move down to reach the last row = M – 1 (M rows, since we are starting from (1, 1) that is not included)
Total number of moves in which we have to move right to reach the last column = N – 1 (n column, since we are starting from (1, 1) that is not included)

Down moves = (M – 1)
Right moves = (N – 1)
Total moves = Down moves + Right moves = (M – 1) + (N – 1) = (M + N – 2) 

Now think of moves as a string of ‘R’ and ‘D’ characters where ‘R’ at any ith index will tell us to move ‘Right’ and ‘D’ will tell us to move ‘Down’. Now think of how many unique strings (moves) we can make where in total there should be (n – 1 + m – 1) characters and there should be (m – 1) ‘D’ character and (n – 1) ‘R’ character? 

Choosing positions of (n – 1) ‘R’ characters results in the automatic choosing of (m – 1) ‘D’ character positions 

The number of ways to choose positions for (n – 1) ‘R’ character = ^{Total positions} C _{n – 1} = ^{Total positions} C _{m – 1} =

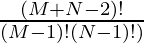
The above equation can be further simplified to:

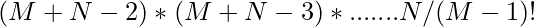
Follow the steps to solve the above problem:

• Define two functions power and modInverse for modular exponentiation and to find the modular inverse of a number respectively.
• Intialize the answer as 1. The formula derived is (M+N-2)*(M+N-3)*…….N/(M-1)!
• Iterate from i=0 to i=M-1 and update the answer as follows:
  • answer = (answer * (N + i)) % MOD
  • answer = (answer * modInverse(i + 1)) % MOD
• Return the answer which denote the count all the possible paths from the top left to the bottom right of an MxN matrix.

Below is the implementation of above approach:

C++

class Solution {
    // Define the MOD constant as 10^9 + 7 for modular arithmetic
    int MOD = 1000000007;

public:
    // Function for modular exponentiation
    long long power(long long x, long long y) {
        long long result = 1;
        x %= MOD;
        while (y > 0) {
            if (y & 1) {
                result = (result * x) % MOD;
            }
            y >>= 1;
            x = (x * x) % MOD;
        }
        return result;
    }

    // Function to find the modular inverse of a number
    long long modInverse(long long n) {
        return power(n, MOD - 2);
    }

    // Function to calculate the number of unique paths
    long long numberOfPaths(int M, int N) {
        // Initialize the answer
        long long answer = 1;

        // Calculate the number of down moves and right moves
        int downMoves = M - 1;
        int rightMoves = N - 1;

        // Apply the combinatorics formula
        for (int i = 0; i < downMoves; i++) {

            answer = (answer * (N + i)) % MOD;

            answer = (answer * modInverse(i + 1)) % MOD;
        }

        return answer;  // Return the final result
    }
};

Java

class Solution {
    // Define the MOD constant as 10^9 + 7 for modular
    // arithmetic
    final int MOD = 1000000007;

    // Function for modular exponentiation
    long power(long x, long y)
    {
        long result = 1;
        x %= MOD;
        while (y > 0) {
            if ((y & 1) == 1) {
                result = (result * x) % MOD;
            }
            y >>= 1;
            x = (x * x) % MOD;
        }
        return result;
    }

    // Function to find the modular inverse of a number
    long modInverse(long n) { return power(n, MOD - 2); }

    // Function to calculate the number of unique paths
    long numberOfPaths(int M, int N)
    {
        // Initialize the answer
        long answer = 1;

        // Calculate the number of down moves and right
        // moves
        int downMoves = M - 1;
        int rightMoves = N - 1;

        // Apply the combinatorics formula
        for (int i = 0; i < downMoves; i++) {
            answer = (answer * (N + i)) % MOD;
            answer = (answer * modInverse(i + 1)) % MOD;
        }

        return answer; // Return the final result
    }
}

Python3

class Solution:
    MOD = 10**9 + 7

    def power(self, x, y):
        result = 1
        x %= self.MOD
        while y > 0:
            if y & 1:
                result = (result * x) % self.MOD
            y >>= 1
            x = (x * x) % self.MOD
        return result

    def compute_mod_inverses(self, M):
        # Initialize an array to store modular inverses
        mod_inverses = [0] * (M + 1)
        mod_inverses[1] = 1

        # Compute modular inverses for numbers from 2 to M
        for i in range(2, M + 1):
            # Use the Extended Euclidean Algorithm to calculate the modular inverse
            mod_inverses[i] = (-(self.MOD // i) *
                               mod_inverses[self.MOD % i]) % self.MOD

        return mod_inverses

    def numberOfPaths(self, M, N):
        answer = 1
        downMoves = M - 1
        rightMoves = N - 1

        # Precompute modular inverses
        mod_inverses = self.compute_mod_inverses(M)

        for i in range(downMoves):
            answer = (answer * (N + i)) % self.MOD
            answer = (answer * mod_inverses[i + 1]) % self.MOD

        return answer

Time Complexity: O(M), This is because the for loop iterates M times
Auxiliary Space: O(1),